Bài 7 trang 6 SBT Hình học 10 Nâng cao

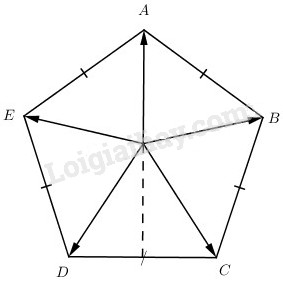
Đề bài

Cho hình ngũ giác đều \(ABCDE\) tâm \(O\). Chứng minh rằng

\(\overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD}  + \overrightarrow {OE}  = \overrightarrow 0 \).

Hãy phát biểu bài toán trong trường hợp n-giác đều.

Lời giải chi tiết

 

Đặt \(\overrightarrow u  = \overrightarrow {OA}  + \overrightarrow {OB}  + \overrightarrow {OC}  + \overrightarrow {OD}  + \overrightarrow {OE} \).

Ta có thể viết:

\(\overrightarrow u  = \overrightarrow {OA}  + (\overrightarrow {OB}  + \overrightarrow {OE} ) + (\overrightarrow {OD}  + \overrightarrow {OC} )\).

Vì \(OA\) là phân giác của góc \(BOE\) và \(OE = OB\) nên tổng \(\overrightarrow {OB}  + \overrightarrow {OE} \) là một vec tơ nằm trên đường thẳng \(OA\).

Tương tự, vec tơ tổng \(\overrightarrow {OC}  + \overrightarrow {OD} \) là một vec tơ cũng nằm trên đường thẳng \(OA\).

Vậy \(\overrightarrow u \) là một vec tơ nằm trên đường thẳng \(OA\).

Chứng minh hoàn toàn tương tự, ta có \(\overrightarrow u \) cũng là một vec tơ nằm trên đường thẳng \(OB\).

Từ đó suy ra \(\overrightarrow u \) phải là vec tơ – không: \(\overrightarrow u  = \overrightarrow 0 \).

Bài toán trong trường hợp n-giác đều:

Nếu \(A_1A_2…A_n\) là n-giác đều tâm \(O\) thì \(\overrightarrow {O{A_1}}  + \overrightarrow {O{A_2}}  + ... + \overrightarrow {O{A_n}}  = \overrightarrow 0 \).

Loigiaihay.com