Bài 5 trang 6 SBT Hình học 10 Nâng cao

Đề bài

Chứng minh rằng với hai vec tơ không cùng phương \(\overrightarrow a \) và \(\overrightarrow b \), ta có

\(|\overrightarrow a | - |\overrightarrow b |< |\overrightarrow a  + \overrightarrow b | <|\overrightarrow a | + |\overrightarrow b |\)

Lời giải chi tiết

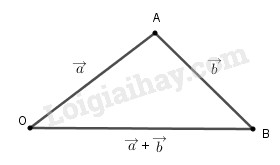
Từ điểm O bất kì, ta vẽ \(\overrightarrow {OA}  = \overrightarrow a ,\,\,\overrightarrow {AB}  = \overrightarrow b \), vì \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương nên ba điểm O, A, B không thẳng hàng.

Khi đó, trong tam giác OAB ta có:

OA-AB < OB< OA+AB

hay \(|\overrightarrow a | - |\overrightarrow b |< |\overrightarrow a  + \overrightarrow b | <|\overrightarrow a | + |\overrightarrow b |\)

Loigiaihay.com