Bài 7 trang 101 SBT Hình học 10 Nâng cao

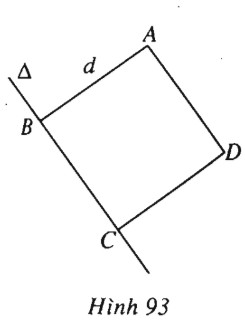
Đề bài

Cho điểm \(A(-1 ; 3)\) và đường thẳng \(\Delta \) có phương trình \(x-2y+2=0\). Dựng hình vuông \(ABCD\) sao cho hai đỉnh \(B, C\) nằm trên \(\Delta \) và các tọa độ của đỉnh \(C\) đều dương.

a) Tìm tọa độ các đỉnh \(B, C, D.\)

b) Tính chu vi và diện tích của hình vuông \(ABCD.\)

Lời giải chi tiết

(h.93).

a) Đường thẳng \(d\) qua \(A\) và vuông góc với \(\Delta \) có phương trình \(2(x+1)+y-3=0\) hay \(2x+y-1=0.\)

Tọa độ của \(B\) là nghiệm của hệ \(\left\{ \matrix{  x - 2y + 2 = 0 \hfill \cr  2x + y - 1 = 0 \hfill \cr}  \right.\).

Giải hệ này ta được \(\left\{ \matrix{  x = 0 \hfill \cr  y = 1 \hfill \cr}  \right.\).

Vậy \(B=(0 ; 1)\)

\(AB = \sqrt {{1^2} + {2^2}}  = \sqrt 5 \).

Tọa độ của \(C\) là nghiệm của hệ \(\left\{ \matrix{  {x_C} - 2{y_C} + 2 = 0 \hfill \cr  \sqrt {x_C^2 + {{({y_C} - 1)}^2}}  = \sqrt 5  \hfill \cr}  \right.\).

Giải hệ này ta được \(\left\{ \matrix{  {x_C} =  - 2 \hfill \cr  {y_C} = 0 \hfill \cr}  \right.\) hoặc \(\left\{ \matrix{  {x_C} = 2 \hfill \cr  {y_C} = 2 \hfill \cr}  \right.\).

Nghiệm đầu bị loại do \(y_C =0\). Vậy \(C=(2 ; 2).\)

Do \(ABCD\) là hình vuông nên \(\overrightarrow {CD}  = \overrightarrow {BA}. \)

Suy ra

\(\left\{ \matrix{  {x_D} - 2 =  - 1 - 0 \hfill \cr  {y_D} - 2 = 3 - 1 \hfill \cr}  \right. \)

\(\Leftrightarrow \left\{ \matrix{  {x_D} = 1 \hfill \cr  {y_D} = 4 \hfill \cr}  \right.\). 

Vậy \(D=(1 ; 4).\)

b) Chu vi hình vuông \(ABCD\) bằng \(4\sqrt 5 \), diện tích bằng \(5.\)

Loigiaihay.com