Bài 11 trang 101 SBT Hình học 10 Nâng cao

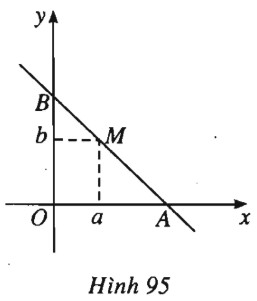
Đề bài

Cho điểm \(M(a; b)\) với \(a > 0, b > 0\). Viết phương trình đường thẳng qua \(M\) và cắt các tia \(Ox, Oy\) lần lượt tại \(A, B\) sao cho tam giác \(OAB\) có diện tích nhỏ nhất.

Lời giải chi tiết

(h.95).

Gọi \(A(x_0 ; 0), B(0 ; y_0).\)

Khi đó, \(x_0 > 0, y_0 > 0\). Phương trình đường thẳng AB là \( \dfrac{x}{{{x_0}}} +  \dfrac{y}{{{y_0}}} = 1\).

\(\begin{array}{l}M \in AB   \Rightarrow    \dfrac{a}{{{x_0}}} +  \dfrac{b}{{{y_0}}} = 1.\\{S_{OAB}} =  \dfrac{1}{2}.OA.OB =  \dfrac{1}{2}{x_0}.{y_0}.\end{array}\)

Ta có

\(1 =  \dfrac{a}{{{x_0}}} +  \dfrac{b}{{{y_0}}} \ge 2\sqrt { \dfrac{{ab}}{{{x_0}{y_0}}}}\)

\(\Rightarrow {x_0}{y_0} \ge 4ab\).

Do đó \({S_{OAB}} =  \dfrac{1}{2}{x_0}{y_0} \ge  \dfrac{1}{2}.4ab = 2ab\).

Dấu “=” xảy ra khi và chỉ khi \( \dfrac{a}{{{x_0}}} =  \dfrac{b}{{{y_0}}} =  \dfrac{1}{2}\) hay \(\left\{ \begin{array}{l}{x_0} = 2a\\{y_0} = 2b\end{array} \right.\).

Vậy diện tích tam giác \(OAB\) nhỏ nhất bằng 2ab khi \(\left\{ \begin{array}{l}{x_0} = 2a\\{y_0} = 2b\end{array} \right.\). Phương trình đường thẳng cần tìm là \( \dfrac{x}{{2a}} +  \dfrac{y}{{2b}} = 1\).

Loigiaihay.com