Bài 68 trang 151 SGK Đại số 10 nâng caoTìm tập xác định của mỗi hàm số sau: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Tìm tập xác định của mỗi hàm số sau: LG a \(y = \sqrt {|{x^2} + 3x - 4| - x + 8} \) Phương pháp giải: Biến đổi tương đương \(\left| f \right| \ge g \Leftrightarrow \left[ \begin{array}{l} Cách khác: Phá dấu GTTĐ và giải các bpt thu được. Lời giải chi tiết: Hàm số đã cho xác định khi và chỉ khi: \(\eqalign{ Xét (1) ta có: \({x^2} + 2x + 4 \ge 0\) \( \Leftrightarrow {x^2} + 2x + 1 + 3 \ge 0\) \( \Leftrightarrow {\left( {x + 1} \right)^2} + 3 \ge 0\) (luôn đúng) Nên tập nghiệm của (1) là R. Xét (2) ta có: \({x^2} + 4x - 12 \le 0 \Leftrightarrow - 6 \le x \le 2\) nên tập nghiệm của (2) là [-6;2]. Hợp hai tập nghiệm của (1) và (2) ta được S=R. Vậy \(S =\mathbb R\). Cách khác: Hàm số đã cho xác định khi và chỉ khi: |x2 + 3x - 4| - x + 8 ≥ 0 (*) + Nếu -4 < x < 1 thì x2 + 3x – 4 < 0, khi đó (*) trở thành: - ( x2 + 3x – 4) – x + 8 ≥ 0 ⇔ - x2 – 4x + 12 ≥ 0 ⇔ -6 ≤ x ≤ 2 Kết hợp điều kiện: - 4 < x < 1 ta được: - 4 < x < 1. * Trường hợp 2. Nếu x ≤ 4 hoặc x ≥ 1 thì x2 + 3x – 4 ≥ 0 . Do đó, bất phương trình (*) trở thành: x2 + 3x – 4 – x + 8 ≥ 0 ⇔ x2 + 2x + 4 ( luôn đúng với mọi x vì x2 + 2x + 4 = (x+1)2 + 3 > 0 mọi x). * Kết hợp cả hai trường hợp,vậy tập xác định của hàm số là D = R. LG b \(y = \sqrt {{{{x^2} + x + 1} \over {|2x - 1| - x - 2}}} \) Lời giải chi tiết: Hàm số đã cho xác định khi và chỉ khi: \({{{x^2} + x + 1} \over {|2x - 1| - x - 2}} \ge 0\) Vì \({x^2} + x + 1 = {x^2} + 2.\frac{1}{2}.x + \frac{1}{4} + \frac{3}{4}\) \( = {\left( {x + \frac{1}{2}} \right)^2} + \frac{3}{4} > 0,\forall x\) nên bất phương trình trên tương đương với bất phương trình \(|2x – 1| - x – 2 > 0\) \(\eqalign{ Vậy \(S = ( - \infty , - {1 \over 3}) \cup (3, + \infty )\). Cách khác:
LG c \(y = \sqrt {{1 \over {{x^2} - 7x + 5}} - {1 \over {{x^2} + 2x + 5}}} \) Lời giải chi tiết: Hàm số đã cho xác định khi và chỉ khi: \(\eqalign{ Vậy \(S = {\rm{[}}0,\,{{7 - \sqrt {29} } \over 2}) \cup ({{7 + \sqrt {29} } \over 2}, + \infty )\) LG d \(\sqrt {\sqrt {{x^2} - 5x - 14} - x + 3}\) Phương pháp giải: Giải bpt \(\sqrt f \ge g \Leftrightarrow \left[ \begin{array}{l} Lời giải chi tiết: Hàm số đã cho xác định khi và chỉ khi: \(\eqalign{ \(\begin{array}{l} Vậy \(S = (-∞; -2] ∪ [23, +∞)\) Loigiaihay.com
|














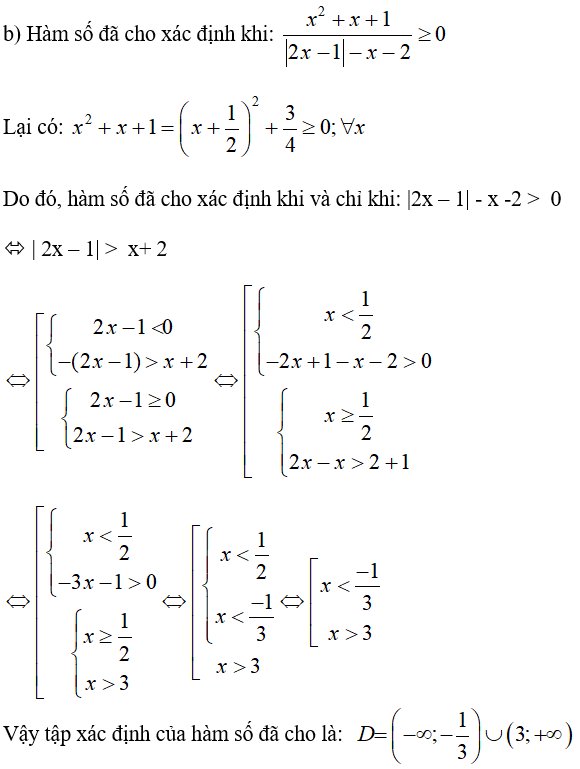






Danh sách bình luận