Bài 65 trang 132 Sách bài tập Hình học lớp 12 Nâng caoa)Tìm tập hợp các điểm cách đều ba điểm A(1;1;1), B(-1;2;0), C(2;-3;2). Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
LG a Tìm tập hợp các điểm cách đều ba điểm A(1;1;1), B(-1;2;0), C(2;-3;2). Lời giải chi tiết: Điểm M(x ; y ; z) cách đều ba điểm A, B, C khi và chỉ khi \(\left\{ \matrix{ M{A^2} = M{B^2} \hfill \cr M{A^2} = M{C^2} \hfill \cr} \right.\)
Vậy tập hợp điểm M(x; y; z) là đường thẳng giao tuyến của hai mặt phẳng lần lượt có phương trình (1) và (2). Đường thẳng đó có phương trình là: \(\left\{ \matrix{ x = - 8 - 3t \hfill \cr y = t \hfill \cr z = 15 + 7t \hfill \cr} \right.\) Nó chính là trục của đường tròn ngoại tiếp tam giác ABC. LG b Tìm quỹ tích các điểm M cách đều hai trục tọa độ Ox, Oy và điểm A(1;1;0). Lời giải chi tiết: Xét điểm M(x ; y ; z). Khi đó khoảng cách dx từ M tới trục Ox là \({d_x} = {{\left| {\left[ {\overrightarrow {OM} ,\overrightarrow i } \right]} \right|} \over {\left| {\overrightarrow i } \right|}} = \sqrt {{y^2} + {z^2}} .\) khoảng cách dy từ M tới trục Oy là \({d_y} = {{\left| {\left[ {\overrightarrow {OM} ,\overrightarrow j } \right]} \right|} \over {\left| {\overrightarrow j } \right|}} = \sqrt {{x^2} + {z^2}} .\) Mặt khác \(MA = \sqrt {{{(x - {\rm{ 1}})}^2} + {\rm{ }}{{\left( {y{\rm{ }} - {\rm{ 1}}} \right)}^2} + {\rm{ }}{z^2}.} \) Vậy M là một điểm của quỹ tích khi \(\left\{ \matrix{ {y^2} + {z^2} = {x^2} + {z^2} \hfill \cr {y^2} + {z^2} = {x^2} + {y^2} + {z^2} - 2(x + y) + 2 \hfill \cr} \right.\) \(\Leftrightarrow \left\{ \matrix{ {x^2} = {y^2} (1) \hfill \cr {x^2} - 2(x + y) + 2 = 0. (2) \hfill \cr} \right.\) Từ (1) suy ra x = y hoặc x = -y. Khi x = y, phương trình (2) có dạng: \({x^2} - 4x + 2 = 0 \Rightarrow x = 2 \pm \sqrt 2 .\) Trong trường hợp này, quỹ tích M là những điểm (x; y; z) mà: \(\left\{ \matrix{ x = 2 + \sqrt 2 \hfill \cr y = 2 + \sqrt 2 \hfill \cr z = t \hfill \cr} \right.\) (3) và \(\left\{ \matrix{ x = 2 - \sqrt 2 \hfill \cr y = 2 - \sqrt 2 \hfill \cr z = t \hfill \cr} \right.\) (4) Khi \(x = - y\), phương trình (2) trở thành: \({x^2} + 2 = 0\). Điều này không xảy ra. Vậy quỹ tích cầm tìm là hai đường thẳng có phương trình (3) và (4) Loigiaihay.com
|














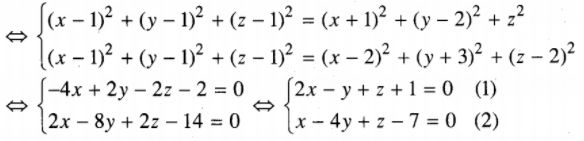






Danh sách bình luận