Bài 55 trang 14 SBT Hình học 10 Nâng caoGiải bài 55 trang 14 sách bài tập Hình học 10 Nâng cao. Cho G là trọng tâm tam giác ABC. Trên cạnh AB lấy hai điểm M và N sao cho AM=MN=NB... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
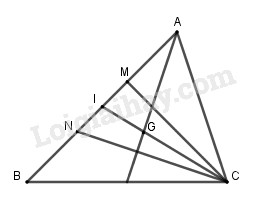
Cho \(G\) là trọng tâm tam giác \(ABC\). Trên cạnh \(AB\) lấy hai điểm \(M\) và \(N\) sao cho \(AM=MN=NB\). LG a Chứng tỏ rằng \(G\) cũng là trọng tâm tam giác \(MNC\). Lời giải chi tiết:
Gọi \(I\) là trung điểm \(MN\) thì \(I\) cũng là trung điểm \(AB\), do đó \(\overrightarrow {GM} + \overrightarrow {GN} = 2\overrightarrow {GI} = \overrightarrow {GA} + \overrightarrow {GB} \) Suy ra \(\overrightarrow {GM} + \overrightarrow {GN} + \overrightarrow {GC} \) \(= \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \). Vậy \(G\) cũng là trọng tâm của tam giác \(MNC.\) LG b Đặt \(\overrightarrow {GA} = \overrightarrow a ,\,\,\overrightarrow {GB} = \overrightarrow b \). Hãy biểu thị các vec tơ sau đây qua \(\overrightarrow a \) và \(\overrightarrow b \): \(\overrightarrow {GC} ,\,\overrightarrow {AC} ,\,\overrightarrow {GM} ,\,\overrightarrow {CN} \). Lời giải chi tiết: Ta có: \(\begin{array}{l} \(\begin{array}{l}\overrightarrow {GM} = \overrightarrow {GA} + \overrightarrow {AM} \\ = \overrightarrow {GA} + \frac{1}{3}\overrightarrow {AB} \\ = \overrightarrow {GA} + \frac{1}{3}\left( {\overrightarrow {GB} - \overrightarrow {GA} } \right)\\= \overrightarrow a + \dfrac{1}{3}(\overrightarrow b - \overrightarrow a ) \\= \dfrac{{2\overrightarrow a + \overrightarrow b }}{3}.\\\overrightarrow {CN} = \overrightarrow {CA} + \overrightarrow {AN} \\ = - \overrightarrow {AC} + \frac{2}{3}\overrightarrow {AB} \\= - \overrightarrow {AC} + \frac{2}{3}\left( {\overrightarrow {GB} - \overrightarrow {GA} } \right)\\ = 2\overrightarrow a + \overrightarrow b + \dfrac{2}{3}(\overrightarrow b - \overrightarrow a )\\ = \dfrac{{4\overrightarrow a + 5\overrightarrow b }}{3}.\end{array}\) Loigiaihay.com
|




















Danh sách bình luận