Bài 54 trang 145 SGK Đại số 10 nâng caoGiải các bất phương trình sau: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
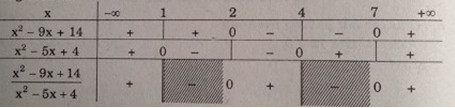
Giải các bất phương trình sau: LG a \({{{x^2} - 9x + 14} \over {{x^2} - 5x + 4}} > 0\) Phương pháp giải: Tìm nghiệm và lập bảng xét dấu các tam thức bậc hai vế trái. Từ đó suy ra tập nghiệm. Lời giải chi tiết: Ta có: \(\eqalign{ Bảng xét dấu:
Vậy \(S = (-∞, 1) ∪ (2, 4) ∪ (7, +∞)\) LG b \({{ - 2{x^2} + 7x + 7} \over {{x^2} - 3x - 10}} \le - 1\) Phương pháp giải: Biến đổi bpt làm xuất hiện các tam thức bậc hai. Xét dấu suy ra tập nghiệm. Lời giải chi tiết: Ta có: \(\eqalign{ Ta lại có: \(\eqalign{ Bảng xét dấu:
LG c (2x + 1)(x2 + x – 30) ≥ 0 Lời giải chi tiết: Ta có: \(\begin{array}{l} Bảng xét dấu:
Vậy \(S = {\rm{[}} - 6,\, - {1 \over 2}{\rm{]}} \cup {\rm{[}}5,\, + \infty )\) LG d x4 – 3x2 ≤ 0 Lời giải chi tiết: Ta có: \(\eqalign{ Vậy \(S = {\rm{[}} - \sqrt 3 ,\,\sqrt 3 {\rm{]}}\) Loigiaihay.com
|














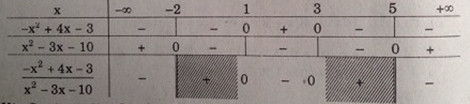 Vậy \(S = (-∞, -2) ∪ [1, 3] ∪ (5, +∞)\)
Vậy \(S = (-∞, -2) ∪ [1, 3] ∪ (5, +∞)\)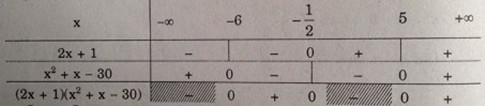






Danh sách bình luận