Bài 5 trang 99 SGK Hình học 12

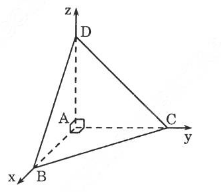
LG a

Tính thể tích tứ diện $ABCD$.

Phương pháp giải:

Chọn hệ toạ độ gốc là điểm $A$, các đường thẳng $AB, AC, AD$ theo thứ tự là các trục $Ox, Oy, Oz$.

Xác định tọa độ các điểm A, B, C, D.

a) ${V_{ABCD}} = \dfrac{1}{6}AB.AC.AD$.

Lời giải chi tiết:

Chọn hệ toạ độ gốc là điểm $A$, các đường thẳng $AB, AC, AD$ theo thứ tự là các trục $Ox, Oy, Oz$.

Ta có: $A(0; 0; 0), B(3; 0; 0);C(0; 4; 0), D(0; 0; 4)$

Ta có: $\overrightarrow {AB}  = (3; 0; 0) \Rightarrow AB = 3$

           $\overrightarrow {AC}  = (0; 4; 0)  \Rightarrow AC = 4$

           $\overrightarrow {AD}  = (0; 0; 4) \Rightarrow AD = 4$

$V_{ABCD}$ = ${1 \over 6}AB.AC.AD = 8 (cm^3)$

LG b

Tính khoảng cách từ điểm $A$ tới mặt phẳng $(BCD)$.

Phương pháp giải:

Viết phương trình mặt phẳng (BCD) ở dạng đoạn chắn $\dfrac{x}{a} + \dfrac{y}{b} + \dfrac{z}{c} = 1$ và sử dụng công thức tính khoảng cách từ 1 điểm đến một mặt phẳng.

Khoảng cách từ điểm $M\left( {{x_0};{y_0};{z_0}} \right)$ đến mặt phẳng $\left( P \right):\,\,Ax + By + Cz + D = 0\,\,\left( {{A^2} + {B^2} + {C^2} > 0} \right)$ là: $d\left( {M;\left( P \right)} \right) = \dfrac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}$

Lời giải chi tiết:

Áp dụng công thức phương trình mặt phẳng theo đoạn chắn, ta có phương trình mặt phẳng $(BDC)$ là:

${x \over 3} + {y \over 4} + {z \over 4} = 1 \Leftrightarrow 4x + 3y + 3z - 12 = 0$

Từ đây ta có: $d(A, (BDC)) ={{\left| {12} \right|} \over {\sqrt {{4^2} + {3^2} + {3^2}} }} = {{12} \over {\sqrt {34} }}$

Loigiaihay.com