Bài 5 trang 53 SGK Hình học 11

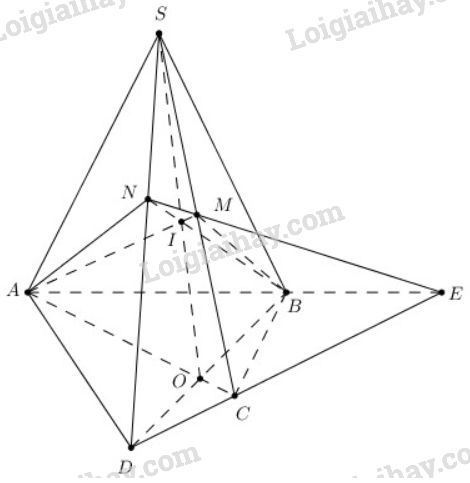
Đề bài

Cho tứ giác \(ABCD\) nằm trong mặt phẳng \((α)\) có hai cạnh \(AB\) và \(CD\) không song song. Gọi \(S\) là điểm nằm ngoài mặt phẳng \((α)\) và \(M\) là trung điểm đoạn \(SC\).

a) Tìm giao điểm \(N\) của đường thẳng \(SD\) và mặt phẳng \((MAB)\).

b) Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Chứng minh rằng ba đường thẳng \(SO, AM, BN\) đồng quy.

Lời giải chi tiết

a) Trong mặt phẳng \((α)\) vì \(AB\) và \(CD\) không song song nên \(AB ∩ DC = E\)

\( \Rightarrow E ∈ DC\), mà \(DC ⊂ (SDC)\)

\( \Rightarrow E ∈ ( SDC)\).

Trong \((SDC)\) đường thẳng \(ME\) cắt \(SD\) tại \(N\)

\( \Rightarrow N ∈ ME\) mà \(ME ⊂ (MAB)\)

\( \Rightarrow N ∈ ( MAB)\). Lại có \(N ∈ SD \Rightarrow N = SD ∩ (MAB)\)

b) \(O\) là giao điểm của \(AC\) và \(BD\)\( \Rightarrow O\) thuộc \(AC\) và \(BD\), mà \(AC ⊂ ( SAC), BD ⊂ (SBD) \)

\( \Rightarrow O ∈( SAC), O ∈ (SBD)\)

\(\Rightarrow\)  \(O\) là một điểm chung của \((SAC)\) và \((SBD)\)

Mặt khác \(S\) cũng là điểm chung của \((SAC)\) và \((SBD)\)

\(\Rightarrow  (SAC) ∩ (SBD) = SO\)

Trong mặt phẳng \((AEN)\) gọi \(I = AM ∩ BN \Rightarrow I \in AM; I \in BN\)

Mà \(AM ⊂ (SAC) \Rightarrow  I ∈ (SAC) \)

\(BN ⊂ ( SBD) \)\(\Rightarrow  I ∈ (SBD)\).

Như vậy \(I\) là điểm chung của \((SAC)\) và \((SBD)\) nên \(I \in SO\) là giao tuyến của \((SAC)\) và \((SBD)\).

Vậy \(S, I, O\) thẳng hàng hay \(SO, AM, BN\) đồng quy tại \(I\).

Cách khác:

b) Chứng minh \(SO, MA, BN\) đồng quy:

+ Trong mặt phẳng \((SAC) : SO\) và \(AM\) cắt nhau.

+ Trong mp \((MAB) : MA\) và \(BN\) cắt nhau

+ Trong mp \((SBD) : SO\) và \(BN\) cắt nhau.

+ Qua \(AM\) và \(BN\) xác định được duy nhất \((MAB)\), mà \(SO\) không nằm trong mặt phẳng \((MAB)\) nên \(AM; BN; SO\) không đồng phẳng.

Theo kết quả bài tập 3 ta có \(SO, MA, BN\) đồng quy.

Loigiaihay.com