Bài 5 trang 26 SGK Hình học 12Cho hình chóp tam giác O.ABC Quảng cáo
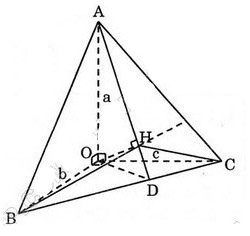
Đề bài Cho hình chóp tam giác \(O.ABC\) có ba cạnh \(OA, OB, OC\) đôi một vuông góc với nhau và \(OA = a, OB = b, OC = c\). Hãy tính đường cao \(OH\) của hình chóp. Video hướng dẫn giải Phương pháp giải - Xem chi tiết +) Gọi \(H\) là trọng tâm của \(\Delta{ABC}\), chứng minh \(OH \, \bot \,(ABC)\). +) Sử dụng các hệ thức lượng trong tam giác vuông tính \(OH\). Lời giải chi tiết
Kẻ \(\displaystyle AD\,\bot \, BC, OH \, \bot \, AD\) ta chứng minh \(\displaystyle OH\) chính là đường cao của hình chóp. \(\displaystyle \begin{array}{l} Vậy \(\displaystyle OH\) chính là đường cao của hình chóp. \(\displaystyle BC \, \bot \, \left( {OAH} \right) \Rightarrow BC \, \bot \, \left( {OAD} \right) \) \(\Rightarrow BC \bot OD\). Tam giác \(OBC\) vuông tại \(O\) nên \(BC = \sqrt {O{B^2} + O{C^2}} = \sqrt {{b^2} + {c^2}} \) Áp dụng hệ thức lượng trong tam giác vuông \(OBC\) ta có: \(\displaystyle OD.BC = OB.OC\) nên \(\displaystyle OD = \frac{{OB.OC}}{{BC}}={{bc} \over {\sqrt {{b^2} + {c^2}} }}\). Áp dụng định lí Pitago trong tam giác vuông \(OAD\) ta có: \(\displaystyle AD = \sqrt {A{O^2} + O{D^2}} \) \(= \sqrt {{a^2} + \dfrac {{b^2}{c^2}} {{b^2} + {c^2}}}\) \(\displaystyle = \sqrt {{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \over {{b^2} + {c^2}}}}\) . Áp dụng hệ thức lượng trong tam giác vuông \(OAD\) ta có: \(\displaystyle OH.AD = OA.OD\) nên \(\displaystyle OH = \dfrac{{OA.OD}}{{AD}}\) \(=\displaystyle {{abc} \over {\sqrt {{b^2} + {c^2}} }}:\sqrt {{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} \over {{b^2} + {c^2}}}} \) \(\displaystyle = {{abc} \over {\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}\). Cách khác: Tam giác \(OBC\) vuông tại \(O\) có \(OD\) là đường cao nên \(\displaystyle \frac{1}{{O{D^2}}} = \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\) Tam giác \(AOD\) vuông tại \(O\) có chiều cao \(OH\) nên \(\displaystyle \frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{D^2}}}\) \(\displaystyle = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\) \( \displaystyle = \frac{1}{{{a^2}}} + \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}} = \frac{{{b^2}{c^2} + {c^2}{a^2} + {a^2}{b^2}}}{{{a^2}{b^2}{c^2}}}\) \( \Rightarrow O{H^2} =\displaystyle \frac{{{a^2}{b^2}{c^2}}}{{{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}}}\) \( \Rightarrow OH = \displaystyle \frac{{abc}}{{\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}\) Chú ý: Ta thấy khi \(OABC\) là tứ diện vuông (\(OA, OB, OC\) đôi một vuông góc) thì: \(\displaystyle \frac{1}{{O{H^2}}} = \frac{1}{{O{A^2}}} + \frac{1}{{O{B^2}}} + \frac{1}{{O{C^2}}}\). Từ nay về sau các em sử dụng kết quả này để các bài toán nhanh chóng hơn. Loigiaihay.com
|




















Danh sách bình luận