Bài 6 trang 26 SGK Hình học 12

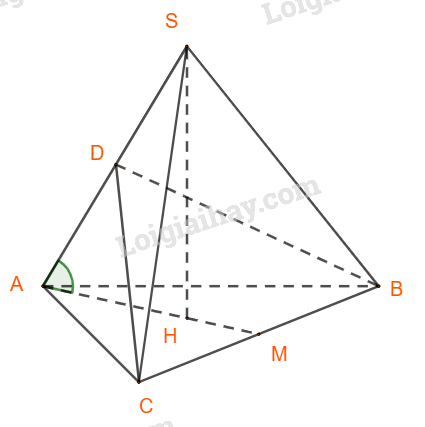
LG a

a) Tính tỉ số thể tích của hai khối chóp $S.DBC$ và $S.ABC$.

Phương pháp giải:

+ Hình chóp có các cạnh bên tạo với đáy góc bằng nhau thì chân đường cao trùng với tâm đường tròn ngoại tiếp đáy.

Qua $B$ kẻ $BD \, \bot  \, SA$, chứng minh mặt phẳng qua $BC$ và vuông góc với $SA$ là $(BCD)$.

+ Sử dụng công thức tỉ số thể tích: $\dfrac{{{V_{S.DBC}}}}{{{V_{S.ABC}}}} = \dfrac{{SD}}{{SA}}.\dfrac{{SB}}{{SB}}.\dfrac{{SC}}{{SC}} = \dfrac{{SD}}{{SA}}$.

Lời giải chi tiết:

Vì hình chóp $\displaystyle S.ABC$ là hình chóp đều nên chân đường cao $\displaystyle H$ là tâm của đường tròn ngoại tiếp đáy.

Do đó $AH$ là hình chiếu của $SA$ lên $(ABC)$ nên góc giữa $SA$ và $(ABC)$ bằng góc giữa $SA$ và $AH$ hay góc $\displaystyle SAH = 60^0$.

Gọi $\displaystyle M$ là trung điểm của cạnh $\displaystyle BC$ thì $\displaystyle AM$ là đường cao của tam giác đều $\displaystyle ABC$:

$\displaystyle AM  = AB\sin {60^0}= {{a\sqrt 3 } \over 2}$

$\displaystyle AH = {2 \over 3}.AM = {{a\sqrt 3 } \over 3}$

$\displaystyle SA = {{AH} \over {c{\rm{os}}{{60}^0}}}$ = $\displaystyle {{2a\sqrt 3 } \over 3}=SB$

Xét tam giác vuông $SBM$ ta có: $\displaystyle SM = \sqrt {S{B^2} - B{M^2}}$ $= \sqrt {\dfrac{{12{a^2}}}{9} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt {39} }}{6}$.

Qua $B$ kẻ $\displaystyle BD \, \bot  \, SA$, khi đó ta có: 

$\displaystyle \begin{array}{l} \left\{ \begin{array}{l} BC \,  \bot  \, AM\\ BC  \, \bot  \, SH \end{array} \right. \Rightarrow BC \bot \left( {SAM} \right) \Rightarrow BC \,  \bot  \, SA\\ \left\{ \begin{array}{l} SA \,  \bot  \, BC\\ SA  \, \bot  \, BD \end{array} \right. \Rightarrow SA \, \bot  \, \left( {BCD} \right) \end{array}$

Khi đó mặt phẳng $(BCD)$ đi qua $BC$ và vuông góc với $SA.$

$\displaystyle SA  \, \bot  \, \left( {BCD} \right) \Rightarrow SA  \, \bot \,  DM$

Xét tam giác vuông $ADM$ có: $\displaystyle DM = AM.\sin 60 = \frac{{a\sqrt 3 }}{2}.\frac{{\sqrt 3 }}{2} = \frac{{3a}}{4}$

Xét tam giác vuông $SDM$ có: $\displaystyle SD = \sqrt {S{M^2} - D{M^2}}  = \frac{{5\sqrt 3 }}{{12}}a$

Áp dụng công thức tỉ số thể tích trong bài tập 4, 3 (trang 37 SGK) ta được:

$\displaystyle {{{V_{S.DBC}}} \over {{V_{S.ABC}}}} = {{SD} \over {SA}}.{{SB} \over {SB}}.{{SC} \over {SC}}$ $\displaystyle = {{5a\sqrt 3 } \over {12}}:{{2a\sqrt 3 } \over 3} = {5 \over 8}$

LG b

b) Tính thể tích của khối chóp $S.DBC$.

Phương pháp giải:

Tính thể tích khối chóp $S.ABC$ sau đó tính thể tích khối chóp $S.DBC$.

Lời giải chi tiết:

Ta có: $\displaystyle S_{ABC} = \frac{1}{2}AB.AC.\sin {60^0}$= $\displaystyle {{{a^2}\sqrt 3 } \over 4}$

$\displaystyle SH = AH.\tan 60^0 = a$

$\displaystyle \Rightarrow {V_{S.ABC}} = {1 \over 3}.SH.{S_{ABC}}$ $= \dfrac{1}{3}.a.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 3 }}{{12}}$

Từ kết quả câu a) ta có:

$\displaystyle {V_{S.DBC}} = {5 \over 8}.{V_{S.ABC}}$ $\displaystyle  \Rightarrow {V_{S.BDC}} = {5 \over 8}.{{{a^3}\sqrt 3 } \over {12}}$

$\displaystyle  \Rightarrow {V_{S.DBC}} = {{5{a^3}\sqrt 3 } \over {96}}$

Loigiaihay.com