Bài 44 trang 130 SGK Toán 9 tập 2

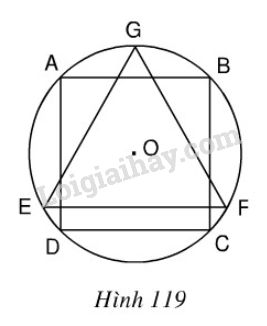
Đề bài

Cho hình vuông $ABCD$ nội tiếp đường tròn tâm $O$, bán kính $R$ và $GEF$ là tam giác đều nội tiếp đường tròn đó, $EF$ là dây song song với $AB$ (h.119). Cho hình đó quay quanh trục $GO$. Chứng minh rằng:

a) Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.

b) Bình phương diện tích toàn phần của hình trụ bằng tích của diện tích hình cầu và diện tích toàn phần của hình nón.

Lời giải chi tiết

Khi quay hình vẽ quanh trục $GO$ ta được:

a) Vì ABCD là hình vuông nên AB = BC =AD = CD; $AC \bot BD$ ( Tính chất)

Áp dụng định lí Pytago trong tam giác vuông OAB, ta có: $AB = \sqrt {OA^2+OB^2}=\sqrt {2R^2}=R\sqrt2.$

Thể tích hình trụ được tạo bởi hình vuông $ABCD$ là:

$\displaystyle V = \pi {\left( {{{AB} \over 2}} \right)^2}.BC$ 

$\eqalign{ & \Rightarrow V = \pi {\left( {{{R\sqrt 2 } \over 2}} \right)^2}.R\sqrt 2 \cr & = \pi .{{2{{\rm{R}}^2}} \over 4}.R\sqrt 2 = {{\pi {{\rm{R}}^3}\sqrt 2 } \over 2} \cr & \Rightarrow {V^2} = \left( {{{\pi {R^3}\sqrt 2 } \over 2}} \right)^2 = {{{\pi ^2}{R^6}} \over 2}(1) \cr}$

Thể tích hình cầu có bán kính $R$ là: $\displaystyle {V_1} = {4 \over 3}\pi {R^3}$ 

Thể tích hình nón có bán kính đường tròn đáy bằng $\displaystyle {{EF} \over 2}$ là:

 $\displaystyle {V_2} = {1 \over 3}\pi {\left( {{{EF} \over 2}} \right)^2}.GH$

Với $EF = R\sqrt3$ (cạnh tam giác đều nội tiếp trong đường tròn $(O;R)$)

và $\displaystyle GH = {{EF\sqrt 3 } \over 2} = {{R\sqrt {3.} \sqrt 3 } \over 2} = {{3R} \over 2}$ 

Thay vào V₂, ta có: $\displaystyle {V_2} = {1 \over 3}\pi {\left( {{{R\sqrt 3 } \over 2}} \right)^2}.{{3{\rm{R}}} \over 2} = {3 \over 8}\pi {R^3}$ 

Ta có: $\displaystyle {V_1}{V_2} = {4 \over 3}\pi {R^3}.{3 \over 8}\pi {R^3} = {{{\pi ^2}{R^6}} \over 2}(2)$

So sánh (1) và (2) ta được : ${V^2} = {V_1}.{V_2}$

b) Diện tích toàn phần của hình trụ có bán kính $\displaystyle {{AB} \over 2}$ là: 

$\eqalign{ & S = 2\pi \left( {{{AB} \over 2}} \right).BC + 2\pi {\left( {{{AB} \over 2}} \right)^2} \cr & S = 2\pi .{{R\sqrt 2 } \over 2}R\sqrt 2 + 2\pi {\left( {{{R\sqrt 2 } \over 2}} \right)^2} \cr & S = 2\pi {R^2} + \pi {R^2} = 3\pi {R^2} \cr & \Rightarrow {S^2} = {\left( {3\pi {R^2}} \right)^2} = 9{\pi ^2}.{R^4}(1) \cr}$ 

Diện tích mặt cầu có bán kính $R$ là: ${S_1} = {\rm{ }}4\pi {R^2}$ (2)

Diện tích toàn phần của hình nón là: 

$\displaystyle {S_2} = \pi {{EF} \over 2}.FG + \pi {\left( {{{EF} \over 2}} \right)^2}$

$\displaystyle = \pi {{R\sqrt 3 } \over 2}.R\sqrt 3  + \pi {\left( {{{R\sqrt 3 } \over 2}} \right)^2} = {{9\pi {R^2}} \over 4}$ 

Ta có: $\displaystyle {S_1}{S_2} = 4\pi {R^2}.{{9\pi {R^2}} \over 4} = 9{\pi ^2}{R^4}(2)$

So sánh (1) và (2) ta có: ${S^2} = {\rm{ }}{S_1}.{\rm{ }}{S_2}$

Loigiaihay.com