Lý thuyết Ôn tập chương 4. Hình trụ - Hình nón - Hình cầuLý thuyết Ôn tập chương 4. Hình trụ - Hình nón - Hình cầu Quảng cáo
1. Hình trụ 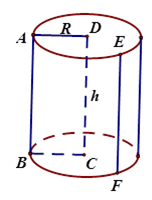 Cho hình trụ có bán kính đáy $R$ và chiều cao $h$. Khi đó : + Diện tích xung quanh : ${S_{xq}} = 2\pi Rh$ . + Diện tích đáy : ${S_đ} = \pi {R^2}$. + Diện tích toàn phần : \({S_{tp}} = {S_{xq}} + 2.{S_đ} = 2\pi Rh + 2\pi {R^2}\) . + Thể tích : $V = \pi {R^2}h$. 2. Hình nón 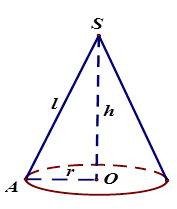 Cho hình nón có bán kính đáy $R = OA$, đường sinh $l = SA$, chiều cao $h = SO$. Khi đó : + Diện tích xung quanh: ${S_{xq}} = \pi Rl.$ + Diện tích đáy : \({S_d} = \pi {R^2}\) + Diện tích toàn phần: ${S_{tp}} = {S_{xq}} + {S_đ} = \pi Rl + \pi {R^2}.$ + Thể tích: $V = \dfrac{1}{3}\pi {R^2}h.$ + Công thức liên hệ : ${R^2} + {h^2} = {l^2}$ 3. Hình nón cụt 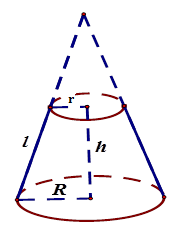 Cho hình nón cụt có các bán kính đáy là $R$ và $r,$ chiều cao $h,$ đường sinh $l.$ + Diện tích xung quanh: ${S_{xq}} = \pi (R + r)l.$ + Diện tích toàn phần: ${S_{tp}} = \pi (R + r)l + \pi {R^2} + \pi {r^2}.$ + Thể tích: $V = \dfrac{1}{3}\pi h({R^2} + Rr + {r^2}).$ 4. Hình cầu 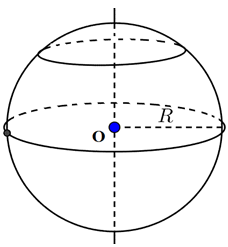 Định nghĩa - Khi quanh nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định ta thu được một hình cầu. - Nửa đường tròn trong phép quay nói trên tạo thành một mặt cầu. - Điểm O gọi là tâm, R là bán kính của hình cầu hay mặt cầu đó. Chú ý: - Khi cắt hình cầu bởi một mặt phẳng ta được một hình tròn. - Khi cắt mặt cầu bán kính $R$ bởi một mặt phẳng ta được một đường tròn, trong đó : + Đường tròn đó có bán kính $R$ nếu mặt phẳng đi qua tâm (gọi là đường kính lớn). + Đường tròn đó có bán kính bé hơn \(R\) nếu mặt phẳng không đi qua tâm. Diện tích và thể tích Cho hình cầu bán kính $R.$ - Diện tích mặt cầu :$S = 4\pi {R^2}$ . - Thể tích hình cầu : \(V = \dfrac{4}{3}\pi {R^3}\).  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
