Bài 43 trang 83 SGK Toán 9 tập 2Cho đường tròn (O) Quảng cáo
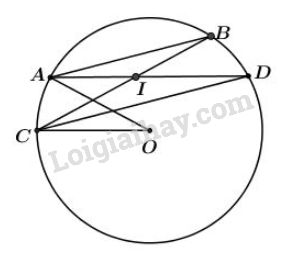
Đề bài Cho đường tròn \((O)\) và hai dây cung song song \(AB,\, CD\) (\(A\) và \(C\) nằm trong cùng một nửa mặt phẳng bờ \(BD\)); \(AD\) cắt \(BC\) tại \(I\). Chứng minh \(\widehat{AOC }= \widehat{AIC }.\) Video hướng dẫn giải Phương pháp giải - Xem chi tiết +) Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn. +) Hai cung bị chắn giữa hai dây song song thì bằng nhau Lời giải chi tiết Vì \(AB // CD\) nên\(\overparen{AC}=\overparen{BD}\) ( 2 cung chắn giữa 2 dây song song thì bằng nhau) (1) Ta có: \(\widehat{AIC}\) là góc có đỉnh ở trong đường tròn chắn cung \(AC\) và cung \(BD\) \(\Rightarrow \widehat{AIC }= \dfrac{sđ\overparen{AC}+sđ\overparen{BD}}{2}\) Theo (1) suy ra \(\widehat{AIC }=\dfrac{sđ\overparen{AC}+sđ\overparen{AC}}{2}\)\(=\dfrac{2.sđ\overparen{AC}}{2}= sđ\overparen{AC}\) (3) Mà \(\widehat{AOC }= sđ\overparen{AC}\) (góc ở tâm chắn cung \(\overparen{AC}\)) (4) Từ (3), (4), ta có \(\widehat{AOC } = \widehat{AIC }\) (đpcm).
|




















Danh sách bình luận