Đề kiểm tra 15 phút - Đề số 2 - Bài 5 - Chương 3 - Hình học 9

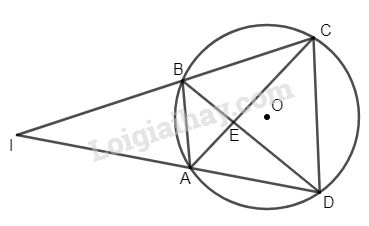
Đề bài

Lấy các điểm A, B, C, D theo thứ tự đó trên đường tròn (O) sao cho số đo các cung: cung AB, cung CD lần lượt là 60º, 120º.

a) Chứng minh rằng: $AC \bot BD$.

b) Gọi I là giao điểm của đường thẳng AD và BC. Tính góc AIB.

Lời giải chi tiết

a) Gọi E là giao điểm của AC và BD. Ta có:

$\widehat {AEB} = \dfrac{{sd\overparen{AB} + sd\overparen{CD}} }{ 2}$$\,= \dfrac{{60^\circ  + 120^\circ }}{ 2} = 90^\circ$ ( góc có đỉnh bên trong đường tròn)

$\Rightarrow$ AC vuông góc BD.

b) $\widehat {AIB} = \dfrac{{sd\overparen{CD} + sd\overparen{AB}} }{ 2}$$\, =\dfrac {{120^\circ  - 60^\circ }}{ 2} = 30^\circ$ ( góc có đỉnh bên ngoài đường tròn).

 Loigiaihay.com