Bài 41 trang 62 SBT Hình học 12 Nâng cao

Đề bài

Một mặt phẳng \(\left( \alpha  \right)\) đi qua hai đường sinh của hình nón, cắt mặt đáy hình nón theo một dây cung có độ dài gấp k lần đường cao hình nón. Tính góc \(\varphi \) giữa mặt phẳng \(\left( \alpha  \right)\) và mặt đáy hình nón nếu \(\varphi \) bằng nửa góc tạo bởi hai đường sinh của hình nón nằm trên mp(\(\alpha \)).

Lời giải chi tiết

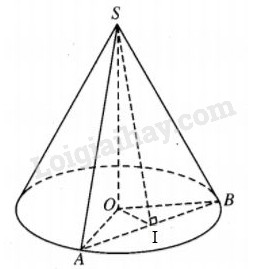
Giả sử O là tâm của đáy hình nón và mặt phẳng \(\left( \alpha  \right)\) đi qua hai đường sinh SA, SB.

Gọi I là trung điểm của AB thì \(OI \bot AB\) và \(SI \bot AB,\) từ đó \(\widehat {SIO}\) = \(\varphi \). Theo giả thiết \(\varphi \) = \(\widehat {ISB}\).

Từ tam giác vuông SIO, ta có \(\sin \varphi  = {{SO} \over {SI}}\;\;\;\;\;\;\;\;\;\;\;\;\,(1)\)

Từ tam giác vuông SIB, ta cũng có \(\tan \varphi  = {{IB} \over {SI}}\;\;\;\;\;(2)\)

Từ (1) và (2) suy ra \({{\sin \varphi } \over {\tan \varphi }} = {{SO} \over {IB}} = {{SO} \over {{k \over 2}SO}} = {2 \over k}.\) 

Vậy \(\cos \varphi  = {2 \over k}.\)

Loigiaihay.com