Bài 4 trang 65 SGK Toán 11 tập 1 - Cánh DiềuTừ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông để tạo ra hình vuông mới như Hình 3. Tiếp tục quá trình này đến vô hạn. a) Tính diện tích Sn của hình vuông được tạo thành ở bước thứ n; b) Tính tổng diện tích của tất cả các hình vuông được tạo thành. Quảng cáo
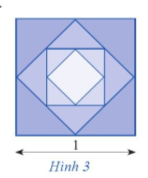
Đề bài Từ hình vuông có độ dài cạnh bằng 1, người ta nối các trung điểm của cạnh hình vuông để tạo ra hình vuông mới như Hình 3. Tiếp tục quá trình này đến vô hạn. a) Tính diện tích \({S_n}\) của hình vuông được tạo thành ở bước thứ n; b) Tính tổng diện tích của tất cả các hình vuông được tạo thành.
Phương pháp giải - Xem chi tiết Sử dụng công thức tính tổng n số hạng đầu của cấp số nhân \({S_n} = {u_1}.\frac{{1 - {q^n}}}{{1 - q}}\). Tổng cấp số nhân lùi vô hạn \(S = \frac{{{u_1}}}{{1 - q}}\). Lời giải chi tiết a) Diện tích hình vuông ban đầu bằng 1.1 = 1 (đvdt). Vì người ta nối các trung điểm của cạnh hình vuông để tạo ra hình vuông mới nên diện tích hình vuông mới sẽ bằng một nửa hình vuông trước. Do đó ta có \({u_1} = {S_1} = 1\), \(q = \frac{1}{2}\). Vậy \({S_n} = 1.\frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{1 - \frac{1}{2}}} = \frac{{1 - {{\left( {\frac{1}{2}} \right)}^n}}}{{\frac{1}{2}}} \) \(= 2 - 2{\left( {\frac{1}{2}} \right)^n} = 2 - {\left( {\frac{1}{2}} \right)^{n - 1}}\). b) Diện tích mỗi hình vuông trên tạo thành một cấp số nhân lùi vô hạn. Sử dụng công thức tính tổng cấp số nhân lùi vô hạn, ta được: \(S = \frac{1}{{1 - \frac{1}{2}}} = 2\).
|




















Danh sách bình luận