Bài 39 trang 36 SGK giải tích 12 nâng caoCùng các câu hỏi như trong bài tập 38 đối với đồ thị của hàm số sau: Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Cùng các câu hỏi như trong bài tập 38 đối với đồ thị của hàm số sau: LG a \(y = {{{x^2} + x - 4} \over {x + 2}}\) Lời giải chi tiết: \(y = x - 1 - {2 \over {x + 2}}\) TXĐ: \(D =\mathbb R\backslash \left\{ { - 2} \right\}\) +) Tìm các đường tiệm cận: \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ + }} y = - \infty \) và \(\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} y = + \infty \) nên \(x = -2\) là tiệm cận đứng. Chú ý: Áp dụng cách chia như bài 38 để viết lại hàm số theo lược đồ dưới đây:
+) Tìm giao điểm hai đường tiệm cận: Gọi I là giao điểm hai đường tiệm cận, tọa độ của I thỏa mãn hệ phương trình \(\left\{ \begin{array}{l} + Công thức chuyển hệ tọa độ trong phép tịnh tiến theo vectơ OI là: \(\left\{ \begin{array}{l}x = X - 2\\y = Y - 3\end{array} \right.\) +) Phương trình của đường cong (C1) trong hệ tọa độ IXY: \(\begin{array}{l}y = x - 1 - \frac{2}{{x + 2}}\\ \Leftrightarrow Y - 3 = X - 2 - 1 - \frac{2}{{X - 2 + 2}}\\ \Leftrightarrow Y = X - \frac{2}{X}\end{array}\) Vậy (C1) trong hệ tọa độ IXY có phương trình \(Y = X - \frac{2}{X}\) Đây là hàm số lẻ nên đồ thị (C1) nhận gốc tọa độ I làm tâm đối xứng. LG b \(y = {{{x^2} - 8x + 19} \over {x - 5}}\) Lời giải chi tiết: Ta có: \(y = x - 3 + \frac{4}{{x - 5}}\) \(\left( {{C_2}} \right)\) + Tiệm cận xiên của đồ thị (C2) là đường thẳng y=x-3 (Vì \(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {x - 3} \right)} \right]\)\( = \mathop {\lim }\limits_{x \to \pm \infty } \left( {x - 3 + \frac{4}{{x - 5}} - x + 3} \right)\) \( = \mathop {\lim }\limits_{x \to \pm \infty } \left( {\frac{4}{{x - 5}}} \right) = 0\)) Tiệm cận đứng của đồ thị là đường thẳng x = 5 (vì \(\mathop {\lim }\limits_{x \to {5^ + }} y = \mathop {\lim }\limits_{x \to {5^ + }} \left( {x - 3 + \frac{4}{{x - 5}}} \right) = + \infty \) và \(\mathop {\lim }\limits_{x \to {5^ - }} y = \mathop {\lim }\limits_{x \to {5^ - }} \left( {x - 3 + \frac{4}{{x - 5}}} \right) = - \infty \)) + Giao điểm I của hai tiệm cận có tọa độ thỏa mãn hệ phương trình \(\left\{ \begin{array}{l}x = 5\\y = x - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 5\\y = 2\end{array} \right.\) Vậy I(5; 2) + Công thức chuyển hệ tọa độ trong phép tịnh tiến theo véc tơ OI là \(\left\{ \begin{array}{l}x = X + 5\\y = Y + 2\end{array} \right.\) + Phương trình của đường cong (C2) trong hệ tọa độ IXY: Ta có: \(\begin{array}{l}y = x - 3 + \frac{4}{{x - 5}}\\ \Leftrightarrow Y + 2 = X + 5 - 3 + \frac{4}{{X + 5 - 5}}\\ \Leftrightarrow Y = X + \frac{4}{X}\end{array}\) Đây là hàm lẻ nên đồ thị (C2) nhận gốc tọa độ I làm tâm đối xứng. Loigiaihay.com
|














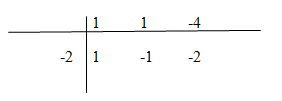






Danh sách bình luận