Bài 38 Trang 36 SGK giải tích 12 nâng caoa) Tìm tiệm cận đứng và tiệm cận xiên của đồ thị của hàm số: b) Xác định giao điểm I của hai tiệm cận trên và viết công thức chuyển hệ tọa độ trong phép tịnh tiến theo véc tơ c) Viết phương trinh của đường cong (C) đối với hệ tọa độ IXY. Từ đó suy ra rằng I là tâm đối xứng của đường cong (C). Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
LG a Tìm tiệm cận đứng và tiệm cận xiên của đồ thị \((C)\) của hàm số: \(y = {{{x^2} - 2x + 2} \over {x - 3}}\) Lời giải chi tiết: Ta có: \(y = \frac{{{x^2} - 2x + 2}}{{x - 3}} = x + 1 + \frac{5}{{x - 3}}\) TXĐ: \(D =\mathbb R\backslash \left\{ 3 \right\}\) Vì \(\mathop {\lim }\limits_{x \to {3^ + }} y = + \infty \) và \(\mathop {\lim }\limits_{x \to {3^ - }} y = - \infty \) nên \(x = 3\) là tiệm cận đứng. \(\mathop {\lim }\limits_{x \to \pm \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to \pm \infty } {5 \over {x - 3}} = 0\) nên \(y = x + 1\) là tiệm cận xiên. Chú ý: Ta thực hiện chia tử cho mẫu theo lược đồ sau:
Ở đó, 1, -2, 2 là các hệ số của tử và 3 là nghiệm cuả mẫu. Cách thực hiện: + Viết 1 -2 2 ở dòng trên, viết 3 ở cột trước đó, hạ 1 thẳng số 1 đầu tiên. + Lấy 1 nhân 3 cộng (-2) được 1, viết 1 thẳng -2. + Lấy 1 nhân 3 cộng 2 bằng 5, viết 5. Từ đó viết được \(y = \frac{{{x^2} - 2x + 2}}{{x - 3}} = x + 1 + \frac{5}{{x - 3}}\). Hoặc các em cũng có thể thực hiện chia đa thức tử cho mẫu cũng được kết quả như vậy. LG b Xác định giao điểm \(I\) của hai tiệm cận trên và viết công thức chuyển hệ tọa độ trong phép tịnh tiến theo véc tơ \(\overrightarrow {OI} \). Lời giải chi tiết: Tọa độ giao điểm \(I(x;y)\) của hai tiệm cận là nghiệm của hệ phương trình \(\left\{ \matrix{ Vậy \(I(3;4)\) là giao điểm của hai tiệm cận trên. Công thức chuyển hệ tọa độ trong phép tịnh tiến theo véc tơ \(\overrightarrow {OI} \) là \(\left\{ \matrix{ LG c Viết phương trình của đường cong \((C)\) đối với hệ tọa độ \(IXY\). Từ đó suy ra rằng \(I\) là tâm đối xứng của đường cong \((C)\). Lời giải chi tiết: Phương trình của đường cong \((C)\) đối với hệ tọa độ \(IXY\) là \(Y + 4 = X + 3 + 1 + {5 \over {X + 3 - 3}}\) \( \Leftrightarrow Y = X + {5 \over X}\) Đây là hàm số lẻ, do đó \((C)\) nhận gốc tọa độ \(I\) làm tâm đối xứng. Loigiaihay.com
|














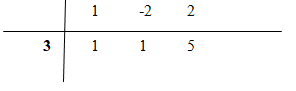






Danh sách bình luận