Bài 37 trang 94 SGK Toán 9 tập 1

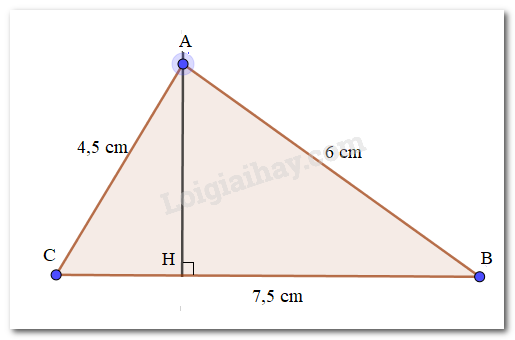
Đề bài

Cho tam giác ABC có AB = 6cm, AC = 4,5cm, BC = 7,5cm.

a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.

b) Hỏi rằng điểm M mà diện tích tam giác MBC bằng diện tích tam giác ABC nằm trên đường nào?

Lời giải chi tiết

a) Xét ∆ABC có $AB^2+AC^2={6^2} + 4,{5^2} = 36 + 20,25$$= 56,25 = 7,{5^2}=BC^2.$

$\Rightarrow ∆ABC$ vuông tại $A$  (định lý Py-ta-go đảo).

 $\eqalign{&Ta \, \, có: tan B = {{AC} \over {AB}} = {{4,5} \over 6} = 0,75 \Rightarrow \widehat B \approx {37^0} \cr & \Rightarrow \widehat C = {90^0} - \widehat B = {53^0}. \cr}$

Áp dụng hệ thức lượng trong tam giác vuông ABC, có:

$AH.BC = AB.AC$

$\displaystyle \Rightarrow AH = {{AB.AC} \over {BC}} = {{4,5.6} \over {7,5}} = 3,6(cm).$

b)

  

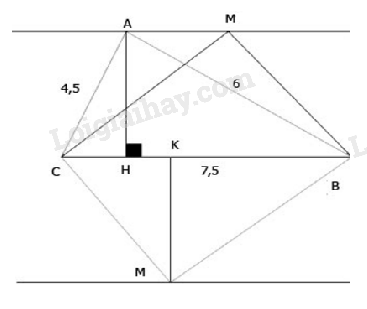
Kẻ $MK \bot BC$ tại $K.$

Ta có: $S_{ABC}=\dfrac{1}{2}AH.BC$ 

$S_{MBC}=\dfrac{1}{2}MK.BC$

Từ đó, $S_{ABC}=S_{MBC} \Leftrightarrow MK= AH=3,6cm.$

Do đó $M$ nằm trên hai đường thẳng song song cách $BC$ một khoảng bằng $3,6 cm$ (hình vẽ).