Bài 36 trang 94 SGK Toán 9 tập 1

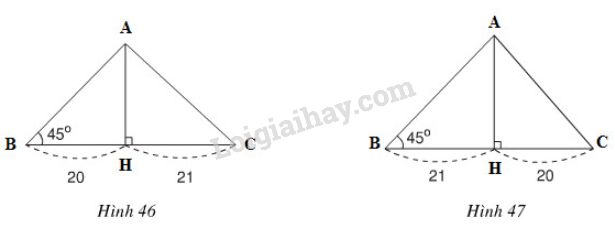
Đề bài

Cho tam giác có một góc bằng 45°. Đường cao chia một cạnh kề với góc đó thành các phần 20cm và 21cm. Tính cạnh lớn trong hai cạnh còn lại (lưu ý có hai trường hợp hình 46 và hình 47)

Lời giải chi tiết

+) Xét hình 46, ta có:

\( BH < HC\,(20cm<21cm) ⇒ AB < AC\) (đường xiên nào có hình chiếu nhỏ hơn thì nhỏ hơn)

\(∆HAB\) vuông tại \(H\) có \(\widehat{ABH} = 45°\) nên là tam giác vuông cân \(⇒ AH = BH = 20 \, (cm).\)

\(∆HAC\) vuông tại \(H,\) theo định lí Py-ta-go có:

\(AC^2=AH^2+HC^2=21^2+20^2=841=29^2.\)

\( \Rightarrow AC = \sqrt {{29^2}}  = 29(cm)\)

Vậy cạnh lớn hơn là \(AC=29cm\)

+) Xét hình 47, ta có:

\( BH > HC\,(21cm>20cm) ⇒ AB > AC\) (đường xiên nào có hình chiếu lớn hơn thì lớn hơn)

\(∆ABH\) vuông tại \(H\) có  \(\widehat{B} = 45°\) nên là tam giác vuông cân \(⇒ AH = BH = 21 \, (cm)\)

Theo định lý Py-ta-go trong tam giác vuông \(ABH\) ta có:

\( AB = \sqrt {{{AH}^2} + {{BH}^2}}\)\(= \sqrt {{{21}^2} + {{21}^2}}  = 21\sqrt 2  \approx 29,7(cm).\)

Vậy cạnh lớn hơn là \(AB=29,7cm\).