Bài 36 trang 61 SBT Hình học 12 Nâng cao

Đề bài

Tìm hình nón có thể tích lớn nhất khi diện tích toàn phần của nó bằng diện tích hình tròn bán kính a cho trước.

Lời giải chi tiết

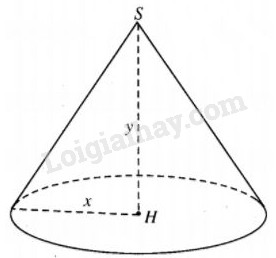
Kí hiệu bán kính đáy và chiều cao hình nón lần lượt là x và y (x, y > 0). Khi đó, diện tích toàn phần của hình nón là

\(\pi x\sqrt {{x^2} + {y^2}}  + \pi {x^2},\)

Theo gia thiết ta có

\(\eqalign{  & \pi x\sqrt {{x^2} + {y^2}}  + \pi {x^2} = \pi {a^2}  \cr  &  \Leftrightarrow x\sqrt {{x^2} + {y^2}}  + {x^2} = {a^2}  \cr  &  \cr} \)

\( \Leftrightarrow x\sqrt {{x^2} + {y^2}}  = {a^2} - {x^2}\) (điều kiện x < a)

\(\eqalign{  &  \Leftrightarrow {x^2}({x^2} + {y^2}) = {a^4} + {x^4} - 2{a^2}{x^2}  \cr  &  \Leftrightarrow {x^2}{y^2} = {a^4} - 2{a^2}{x^2} \Leftrightarrow {x^2} = {{{a^4}} \over {{y^2} + 2{a^2}}} \cr} \)

Khi đó thể tích khối nón là

\(V = {1 \over 3}\pi {{{a^4}} \over {{y^2} + 2{a^2}}}.y = {{\pi {a^4}} \over 3}.{y \over {{y^2} + 2{a^2}}}.\)

Từ đó V đạt giá trị lớn nhất khi và chỉ khi \({{{y^2} + 2{a^2}} \over y}\) đạt giá trị nhỏ nhất.

Ta có \({{{y^2} + 2{a^2}} \over y} = y + {{2{a^2}} \over y} \ge 2\sqrt {y.{{2{a^2}} \over y}}  = 2\sqrt 2 a.\)

Vậy V đạt giá trị lớn nhất khi và chỉ khi \(y = {{2{a^2}} \over y},\) tức là \(y = a\sqrt 2 \), lúc đó \(x = {a \over 2}.\)

Loigiaihay.com