Bài 35 trang 43 SBT Hình học 10 Nâng cao

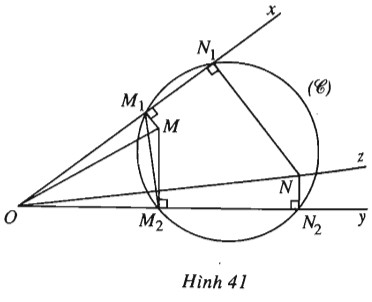
Đề bài

Cho điểm \(M\) nằm trong góc \(\widehat {xOy}\) và gọi \(M_1, M_2\) lần lượt là hình chiếu của \(M\) trên \(Ox, Oy.\)

a) Vẽ đường tròn \((C)\) qua \(M_1, M_2\), đường tròn này cắt hai cạnh \(Ox, Oy\) lần lượt ở \(N_1, N_2\). Kẻ đường thẳng vuông góc với \(Ox\) ở \(N_1\) và đường thẳng vuông góc với \(Oy\) ở \(N_2\), giả sử hai đường thẳng đó cắt nhau ở \(N\). Chứng minh \(ON \bot {M_1}{M_2}\).

b) Chứng minh rằng khi \((C)\) thay đổi nhưng vẫn đi qua \(M_1\) và \(M_2\) thì điểm \(N\) luôn thuộc một tia \(Oz\) cố định và \(\widehat {zOy} = \widehat {MO{N_1}}\).

Lời giải chi tiết

(h.41).

a) Ta có \(\overrightarrow {O{M_1}} .\overrightarrow {O{N_1}}  = \overrightarrow {O{M_2}} .\overrightarrow {O{N_2}} \,\,\,\,\,\,\,\,\,\,(*)\)

Xét tích vô hướng

\(\overrightarrow {ON} .\overrightarrow {{M_1}{M_2}}  = \overrightarrow {ON} .\left( {\overrightarrow {O{M_2}}  - \overrightarrow {O{M_1}} } \right)\)

\(= \overrightarrow {ON} .\overrightarrow {O{M_2}}  - \overrightarrow {ON} .\overrightarrow {O{M_1}} .\)

Do \(\overrightarrow {O{N_1}} \) là hình chiếu của \(\overrightarrow {ON} \) trên Ox nên \(\overrightarrow {ON} .\overrightarrow {O{M_1}}  = \overrightarrow {O{N_1}} .\overrightarrow {O{M_1}} .\)

Tương tự \(\overrightarrow {ON} .\overrightarrow {O{M_2}}  = \overrightarrow {O{N_2}} .\overrightarrow {O{M_2}} \,\,\,\,\,\,\,\,\,\,\,(**)\)

Từ (*), (**) suy ra \(\overrightarrow {ON} .\overrightarrow {{M_1}{M_2}}  = 0\) hay \(ON \bot {M_1}{M_2}\).

b) Theo câu a), \(N\) thuộc tia \(Oz\) cố định (vuông góc với \(M_1M_2\)).

Lại có \(\widehat {zOy} = \widehat {{M_1}{M_2}M}\) (do \(Oz \bot {M_2}{M_1}\,,\,\,Oy \bot {M_2}M\)).

Mặt khác, \(OM_1MM_2\) là tứ giác nội tiếp  (\(\widehat {O{M_1}M} = \widehat {O{M_2}M} = {90^0}\)) nên \(\widehat {{M_1}{M_2}M} = \widehat {{M_1}OM}\). Từ đó suy ra \(\widehat {zOy} = \widehat {MO{N_1}}\).

Loigiaihay.com