Bài 31 trang 60 SBT Hình học 12 Nâng cao

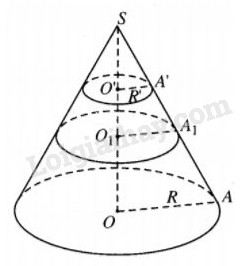
Đề bài

Cho hình nón N có bán kính đáy bằng R, đường cao SO. Một mặt phẳng (P) cố định vuông góc với SO tại O’, cắt hình nón N theo đường tròn có bán kính R’. Mặt phẳng (Q) thay đổi, vuông góc với SO tại điểm O₁ (O₁ nằm giữa O và O’), cắt hình nón theo thiết diện là hình tròn có bán kính x.

Hãy tính x theo R và R’ nếu (Q) chia phần hình nón nằm giữa (P) và đáy hình nón thành hai phần có thể tích bằng nhau.

Lời giải chi tiết

Gọi V₁ là thể tích phần hình nón giữa đỉnh S và mp(P), V₂ là thể tích phần hình nón giữa mặt phẳng (P) và (Q), V₃ là thể tích phần hình nón giữa mặt phẳng (Q) và đáy hình nón đã cho. Khi ấy

\(\eqalign{  & {{{V_1}} \over {{V_1} + {V_2}}} = {\left( {{{R'} \over x}} \right)^3}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(1)  \cr  & {{{V_1} + {V_2} + {V_3}} \over {{V_1} + {V_2}}} = {\left( {{R \over x}} \right)^3}\;\;\;\;\;\;\;\;(2) \cr} \)

Và \({V_3} = {V_2}\;\;\;\;\;\;\;\;\;\;\;\;\;\;(3)\)

Từ (2), (3) suy ra

\({{{V_1} + 2{V_2}} \over {{V_1} + {V_2}}} = {\left( {{R \over x}} \right)^3}\;\;\;\;\;\;\;(4)\)

Từ (1), (4) ta có

\({{2({V_1} + {V_2})} \over {{V_1} + {V_2}}} = {{{R^3} + R{'^3}} \over {{x^3}}} \Leftrightarrow x = \root 3 \of {{{{R^3} + R'{^ 3}} \over 2}} \)

Loigiaihay.com