Bài 3 trang 94 SGK Đại số 10

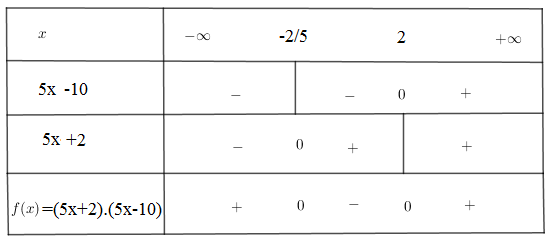
LG a

$|5x - 4| ≥ 6$;

Phương pháp giải:

$\begin{array}{l} \left| {f\left( x \right)} \right| \le a \Leftrightarrow  - a \le f\left( x \right) \le a\\ \left| {f\left( x \right)} \right| \ge a \Leftrightarrow \left[ \begin{array}{l} f\left( x \right) \le  - a\\ f\left( x \right) \ge a \end{array} \right.\\ \left( {a > 0} \right) \end{array}$

Lời giải chi tiết:

$|5x - 4| ≥ 6$

Cách 1:

$\eqalign{ & \Leftrightarrow {(5x - 4)^2} \ge {6^2}\cr& \Leftrightarrow {(5x - 4)^2} - {6^2} \ge 0 \cr  & \Leftrightarrow (5x - 4 - 6)(5x - 4 + 6) \ge 0 \cr  & \Leftrightarrow (5x - 10)(5x + 2) \ge 0 \cr}$

Bảng xét dấu:

Ta có:

$\begin{array}{l} 5x - 10 = 0 \Leftrightarrow x = 2\\ 5x + 2 = 0 \Leftrightarrow x =  - \dfrac{2}{5} \end{array}$

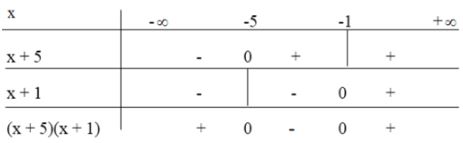
Từ bảng xét dấu cho tập nghiệm của bất phương trình: $T =\left( { - \infty ; - {2 \over 5}} \right] ∪ [2; +∞)$.

Cách 2:

$\begin{array}{l} \left| {5x - 4} \right| \ge 6 \Leftrightarrow \left[ \begin{array}{l} 5x - 4 \ge 6\\ 5x - 4 \le - 6 \end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l} 5x \ge 10\\ 5x \le - 2 \end{array} \right. \Leftrightarrow \left[ \begin{array}{l} x \ge 2\\ x \le - \dfrac{2}{5} \end{array} \right. \end{array}$

Vậy tập nghiệm của bất phương trình: $T =\left( { - \infty ; - {2 \over 5}} \right] ∪ [2; +∞)$.

LG b

$\left | \dfrac{-5}{x+2} \right |<\left | \dfrac{10}{x-1} \right |.$

Lời giải chi tiết:

$\left | \dfrac{-5}{x+2} \right |<\left |\dfrac{10}{x-1} \right |$

Cách 1:

$\eqalign{ & \Leftrightarrow {5 \over {|x + 2|}} < {{10} \over {|x - 1|}} \cr &\left( {DK:x \ne - 2,x \ne 1} \right) \cr&\Leftrightarrow {1 \over {|x + 2|}} < {2 \over {|x - 1|}} \cr  & \Leftrightarrow 2|x + 2| - |x - 1| > 0  \text{     } (1)\cr}$

Bảng xét dấu:

+) Với $x <  - 2$ ta có:

$\begin{array}{l}\left( 1 \right) \Leftrightarrow 2\left( { - x - 2} \right) - \left( { - x + 1} \right) > 0\\ \Leftrightarrow  - 2x - 4 + x - 1 > 0\\ \Leftrightarrow  - x - 5 > 0\\ \Leftrightarrow  - x > 5\\ \Leftrightarrow x <  - 5\end{array}$

Kết hợp với $x <  - 2$ ta được $x <  - 5$.

+) Với $- 2 < x < 1$ ta có:

$\begin{array}{l}\left( 1 \right) \Leftrightarrow 2\left( {x + 2} \right) - \left( { - x + 1} \right) > 0\\ \Leftrightarrow 2x + 4 + x - 1 > 0\\ \Leftrightarrow 3x + 3 > 0\\ \Leftrightarrow 3x >  - 3\\ \Leftrightarrow x >  - 1\end{array}$

Kết hợp với $- 2 < x < 1$ ta được $- 1 < x < 1$

+) Với $x > 1$ ta có:

$\begin{array}{l}\left( 1 \right) \Leftrightarrow 2\left( {x + 2} \right) - \left( {x - 1} \right) > 0\\ \Leftrightarrow 2x + 4 - x + 1 > 0\\ \Leftrightarrow x + 5 > 0\\ \Leftrightarrow x >  - 5\end{array}$

Kết hợp với $x > 1$ ta được $x > 1$.

Vậy bất phương trình có nghiệm $\left[ \begin{array}{l}x <  - 5\\ - 1 < x < 1\\x > 1\end{array} \right.$

Tập nghiệm của bất phương trình là: $T = (-∞; - 5) ∪ (- 1; 1) ∪ (1; +∞)$.

Cách 2:

$\begin{array}{l} \dfrac{5}{{\left| {x + 2} \right|}} < \dfrac{{10}}{{\left| {x - 1} \right|}}\\ \left( {DK:x \ne - 2,x \ne 1} \right)\\ \Leftrightarrow \dfrac{1}{{\left| {x + 2} \right|}} < \dfrac{2}{{\left| {x - 1} \right|}}\\ \Rightarrow \left| {x - 1} \right| < 2\left| {x + 2} \right|\\ \Leftrightarrow {\left( {x - 1} \right)^2} < 4{\left( {x + 2} \right)^2}\\ \Leftrightarrow {x^2} - 2x + 1 < 4\left( {{x^2} + 4x + 4} \right)\\ \Leftrightarrow 3{x^2} + 18x + 15 > 0\\ \Leftrightarrow 3\left( {x + 1} \right)\left( {x + 5} \right) > 0 \end{array}$

Ta có bảng xét dấu:

Xét dấu ta được $\left[ \begin{array}{l}x < - 5\\x > - 1\end{array} \right.$

Kết hợp điều kiện $x\ne -2,x\ne 1$ ta được tập nghiệm của bất phương trình là: $T = (-∞; - 5) ∪ (- 1; 1) ∪ (1; +∞)$.

Loigiaihay.com