Bài 29 trang 43 SBT Hình học 10 Nâng cao

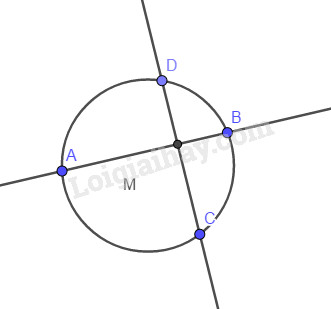
Đề bài

Cho hai đường thẳng \(AB, CD\) cắt nhau ở điểm \(M\). Chứng minh rằng bốn điểm \(A, B, C, D\) cùng thuộc một đường tròn khi và chỉ khi

\(\overrightarrow {MA} .\overrightarrow {MB}  = \overrightarrow {MC} .\overrightarrow {MD} .\)

Lời giải chi tiết

Nếu \(A, B, C, D\) cùng thuộc một đường tròn \((C)\) thì \(\overrightarrow {MA} .\overrightarrow {MB} ,\,\,\overrightarrow {MC} .\overrightarrow {MD} \) cũng bằng phương tích của điểm \(M\) đối với đường tròn \((C)\) nên \(\overrightarrow {MA} .\overrightarrow {MB}  = \overrightarrow {MC} .\overrightarrow {MD} \)

Ngược lại, vẽ đường tròn qua ba điểm \(A, B, C\) và giả sử đường tròn đó cắt đường thẳng \(CD\) ở điểm \(D’\) khác \(C\). Khi đó ta có \(A, B, C, D’\) cùng thuộc một đường tròn nên \(\overrightarrow {MA} .\overrightarrow {MB}  = \overrightarrow {MC} .\overrightarrow {MD'} \)

Nếu có \(\overrightarrow {MA} .\overrightarrow {MB}  = \overrightarrow {MC} .\overrightarrow {MD} \) thì \(\overrightarrow {MC} .\overrightarrow {MD}  = \overrightarrow {MC} .\overrightarrow {MD'} \), suy ra \(\overrightarrow {MC} .\overrightarrow {DD'}  = 0\). Do \(\overrightarrow {MC}  \ne \overrightarrow 0 \) và \(\overrightarrow {DD'} \) cùng phương với \(\overrightarrow {MC} \) nên \(\overrightarrow {DD'}  = \overrightarrow 0 \) hay \(D, D’\) trùng nhau. Vậy \(A, B, C, D\) cùng thuộc một đường tròn.

Loigiaihay.com