Bài 27 trang 88 SGK Toán 9 tập 1

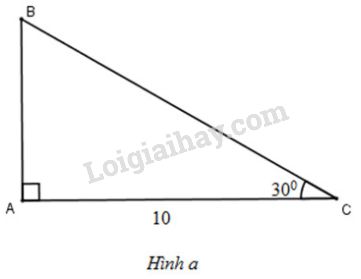
LG a

\(b=10cm;\ \widehat{C}=30^{\circ}\)

Phương pháp giải:

Giải tam giác vuông là đi tìm tất cả các yếu tố (góc và cạnh) chưa biết của tam giác đó.

+) Sử dụng các hệ thức về cạnh và góc trong tam giác vuông: Tam giác \(ABC\) vuông tại \(A\) thì:

\(b=a.\sin B = a . \cos C;\)                  \(b = c. \tan B = c. \cot C;\)

\(c=a.\sin C = a. \cos B;\)                    \(c=b.\tan C = b.\cot B\).  

Lời giải chi tiết:

 Quy ước: Tam giác ABC vuông tại A có a = BC ; b = AC; c = AB

(H.a)

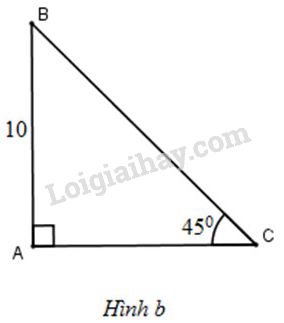
+) Ta có: \(\widehat{B} + \widehat{C}=90^{\circ} \Rightarrow \widehat{B}=90^o -30^{\circ}=60^{\circ}\)

+) Lại có 

\(AB = AC. \tan C=10.tan 30^o=\dfrac{10\sqrt 3}{3} \approx 5,77(cm)\)

\(AC=BC. \cos C \Rightarrow 10=BC. \cos 30^o \Rightarrow BC=\dfrac{10}{\cos 30^o}=\dfrac{20\sqrt 3}{3} \approx 11,55(cm)\).

LG b

\(c=10cm;\ \widehat{C}=45^{\circ}\)

Phương pháp giải:

Giải tam giác vuông là đi tìm tất cả các yếu tố (góc và cạnh) chưa biết của tam giác đó.

+) Sử dụng các hệ thức về cạnh và góc trong tam giác vuông: Tam giác \(ABC\) vuông tại \(A\) thì:

\(b=a.\sin B = a . \cos C;\)                  \(b = c. \tan B = c. \cot C;\)

\(c=a.\sin C = a. \cos B;\)                    \(c=b.\tan C = b.\cot B\).  

Lời giải chi tiết:

(H.b)

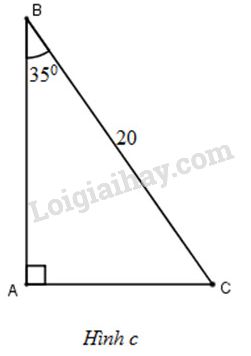
+) Xét tam giác \(ABC\) vuông tại \(A\) có \(AB=10,\ \widehat{C}=45^o\) nên \(ABC\) là tam giác vuông cân tại A \(\Rightarrow \widehat{B}=45^{\circ}; AB=AC=10(cm)\)

+) Lại có: \(AB=BC. \sin C \Rightarrow 10=BC. sin 45^o\)

\(\Rightarrow BC=\dfrac{10}{\sin 45^o}=10\sqrt 2 \approx 14,14(cm).\)

LG c

\(a=20cm;\ \widehat{B}=35^{\circ}\)

Phương pháp giải:

Giải tam giác vuông là đi tìm tất cả các yếu tố (góc và cạnh) chưa biết của tam giác đó.

+) Sử dụng các hệ thức về cạnh và góc trong tam giác vuông: Tam giác \(ABC\) vuông tại \(A\) thì:

 \(b=a.\sin B = a . \cos C;\)                  \(b = c. \tan B = c. \cot C;\)

\(c=a.\sin C = a. \cos B;\)                    \(c=b.\tan C = b.\cot B\).  

Lời giải chi tiết:

 (H.c) 

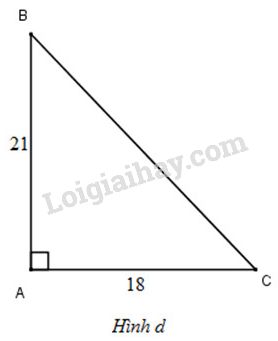
+) Ta có: \(\widehat{C}+ \widehat{B}=90^{\circ} \Rightarrow \widehat{C}= 90^o - \widehat{B}=90^o - 35^{\circ}=55^{\circ}.\) 

+) Lại có: \(AB=BC\cdot cosB=20\cdot cos35^{\circ}\approx 16,383 (cm)\)

                \(AC= BC \cdot sinB=20\cdot sin35^{\circ}\approx 11,472 (cm)\).

LG d

\(c=21cm;\ b=18cm\)

Phương pháp giải:

Giải tam giác vuông là đi tìm tất cả các yếu tố (góc và cạnh) chưa biết của tam giác đó.

+) Sử dụng định lý Pytago: Tam giác \(ABC\) vuông tại \(A\) thì \(BC^2 = AC^2 + AB^2.\)

+) Sử dụng các hệ thức về cạnh và góc trong tam giác vuông: Tam giác \(ABC\) vuông tại \(A\) thì:

 \(b=a.\sin B = a . \cos C;\)                  \(b = c. \tan B = c. \cot C;\)

\(c=a.\sin C = a. \cos B;\)                    \(c=b.\tan C = b.\cot B\).  

Lời giải chi tiết:

(H.d)

Áp dụng định lí Pytago vào tam giác vuông ABC, ta được: \(BC^2=AC^2+AB^2=18^2 +21^2=765\)

\(\Rightarrow BC = \sqrt{765}=3\sqrt{85} \approx 27,66(cm)\)

Lại có:

\(\tan B=\dfrac{AC}{AB}=\dfrac{18}{21} \approx 0,8571\)

Bấm máy tính: SHIFT tan 0,8571 \(\Rightarrow \widehat{B}\approx 41^{\circ}\)

Vì \(\widehat{C }+\widehat{B}=90^o \Rightarrow \widehat{C}= 90^o - 41^o =49^{\circ}\)