Bài 24 trang 103 SBT Hình học 10 Nâng caoGiải bài tập Bài 24 trang 103 SBT Hình học 10 Nâng cao Quảng cáo
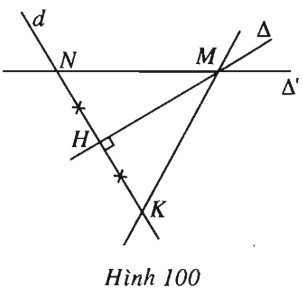
Đề bài Cho hai đường thẳng \(\Delta : \left\{ \begin{array}{l}x = - 2t\\y = 1 + t\end{array} \right. , \Delta ': \left\{ \begin{array}{l}x = - 2 - t'\\y = t'\end{array} \right.\). Viết phương trình đường thẳng đối xứng với \(\Delta \)’ qua \(\Delta \). Lời giải chi tiết (h.100).
Dễ tìm được giao điểm \(M\) của \(\Delta \) và \(\Delta \)’ có tọa độ là \((-6 ; 4)\). Điểm \(N(-2 ; 0)\) thuộc \(\Delta \)’ và \(N\) khác \(M.\) Đường thẳng \(d\) đi qua \(N\) và vuông góc với \(\Delta \) có phương trình \( - 2(x + 2) + y = 0 \Leftrightarrow 2x - y + 4 = 0\). Gọi \(H = d \cap \Delta \), suy ra \(H = \left( { - \dfrac{6}{5} ; \dfrac{8}{5}} \right)\). Do đó tọa độ điểm \(K\) đối xứng với điểm \(N\) qua \(H\) là \(\left( { - \dfrac{2}{5} ; \dfrac{{16}}{5}} \right)\). Đường thẳng cần tìm là đường thẳng \(MK\) và có phương trình \(x+7y-22=0.\) Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
