Bài 20 trang 76 SGK Toán 9 tập 2

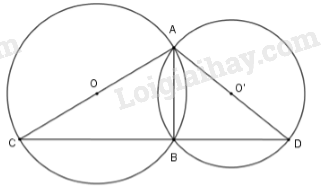
Đề bài

Cho hai đường tròn $(O)$ và $(O')$ cắt nhau tại $A$ và $B$. Vẽ các đường kính $AC$ và $AD$ của hai đường tròn. Chứng minh rằng ba điểm $C, B, D$ thẳng hàng.

Lời giải chi tiết

 

Nối $B$ với 3 điểm $A, C, D$.

Xét đường tròn $\left( O \right)$ có $\widehat {ABC}$ là góc nội tiếp chắn nửa đường tròn nên $\widehat {ABC} = 90^\circ .$

Xét đường tròn $\left( {O'} \right)$ có $\widehat {ABD}$ là góc nội tiếp chắn nửa đường tròn nên $\widehat {ABD} = 90^\circ .$

Suy ra $\widehat {ABC} + \widehat {ABD} = 90^\circ  + 90^\circ  = 180^\circ$ nên $\widehat {CBD} = 180^\circ  \Rightarrow C,B,D$ thẳng hàng.

loigiaihay.com