Bài 2 trang 128 Tài liệu dạy – học Toán 9 tập 1

Giải bài tập Cho tam giác ABC, các đường cao BH và CK. Chứng minh rằng :

Quảng cáo

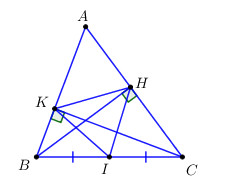
Đề bài

Cho tam giác ABC, các đường cao BH và CK. Chứng minh rằng :

a) Bốn điểm B, C, H, K cùng thuộc một đường tròn.

b) HK < BC.

Phương pháp giải - Xem chi tiết

+) Sử dụng định lí đường trung tuyến trong tam giác vuông chứng minh 4 điểm \(B,\,\,C,\,\,H,\,\,K\) cùng thuộc một đường tròn.

+) Trong một đường tròn, mọi dây cung không đi qua tâm đều nhỏ hơn đường kính của đường tròn đó.

Lời giải chi tiết

Gọi \(I\) là trung điểm của \(BC\).

Xét tam giác vuông BHC có \(IH = \dfrac{1}{2}BC = IB = IC\,\,\left( 1 \right)\) (trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy).

Xét tam giác vuông BKC có \(IK = \dfrac{1}{2}BC = IB = IC\,\,\left( 1 \right)\) (trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng nửa cạnh ấy).

Từ (1) và (2) \( \Rightarrow IH = IK = IB = IC \Rightarrow \) 4 điểm \(B,\,\,C,\,\,H,\,\,K\) cùng thuộc đường tròn tâm \(I\) đường kính \(BC\).

Xét đường tròn \(\left( {I;\dfrac{{BC}}{2}} \right)\) ta có \(BC\) là đường kính, \(HK\) là dây cung không đi qua tâm.

Vậy \(HK < BC\).

Loigiaihay.com