Bài 18 trang 41 SBT Hình học 10 Nâng cao

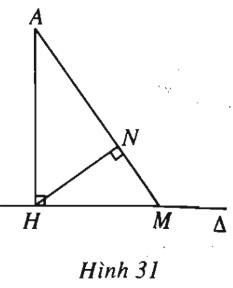
Đề bài

Cho điểm \(A\) cố định nằm ngoài đường thẳng \(\Delta \), \(H\) là hình chiếu của \(A\) trên \(\Delta \). Với mỗi điểm \(M\) trên \(\Delta \), lấy điểm \(N\) trên tia \(AM\) sao cho \(\overrightarrow {AN} .\overrightarrow {AM}  = A{H^2}\). Tìm tập hợp các điểm \(N.\)

Lời giải chi tiết

(h.31). Ta có

\(\overrightarrow {AN} .\overrightarrow {AM}  = {\overrightarrow {AH} ^2}\)

\( \Leftrightarrow \overrightarrow {AN} .\overrightarrow {AM}  = \overrightarrow {AH} .\overrightarrow {AH}  = \overrightarrow {AH} .\overrightarrow {AM} \) ( theo công thức hình chiếu)

\(\eqalign{  &  \Leftrightarrow \overrightarrow {AN} .\overrightarrow {AM}  - \overrightarrow {AH} .\overrightarrow {AM}  = 0  \cr  &  \Leftrightarrow (\overrightarrow {AN}  - \overrightarrow {AH} )\overrightarrow {AM}  = 0  \cr  &  \Leftrightarrow \overrightarrow {HN} .\overrightarrow {AM}  = 0 \cr} \)

Vậy tập hợp các điểm \(N\) là đường tròn đường kính \(AH\).

Loigiaihay.com