tuyensinh247
Trang chủ
Giải toán 10, giải bài tập Toán 10 Nâng cao, đầy đủ đại số giải tích và hình học

Bài 12 trang 73 SGK Hình học 10 nâng cao

Cho tam giác MPQ vuông tại P. Trên cạnh MQ lấy hai điểm E, F sao cho các góc MPE, EPF, FPQ bằng nhau.

Quảng cáo

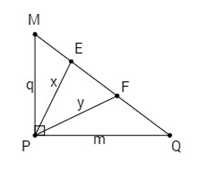
Đề bài

Cho tam giác MPQ vuông tại P. Trên cạnh MQ lấy hai điểm E, F sao cho các góc MPE, EPF, FPQ bằng nhau.

Đặt \(MP = q,\,PQ = m,\,PE = x,\,PF = y\) (h.64).

Trong các hệ thức sau, hệ thức nào đúng ?

(A) \(ME = EF = FQ\);

(B) \(M{E^2} = {q^2} + {x^2} - xq\);

(C) \(M{F^2} = {q^2} + {y^2} - yq\);

(D) \(M{Q^2} = {q^2} + {m^2} - 2qm\).

Lời giải chi tiết

 

Đáp án A: ME, EF, FQ chưa chắc bằng nhau nên A sai.

Đáp án B:

\(\begin{array}{l}
M{E^2} = P{M^2} + P{E^2} - 2PM.PE\cos {30^0}\\
= {q^2} + {x^2} - 2qx.\frac{{\sqrt 3 }}{2}\\
= {q^2} + {x^2} - \sqrt 3 qx
\end{array}\)

nên B sai.

Đáp án C:

Ta có \(M{F^2} = M{P^2} + F{P^2} - 2.MP.FP.\cos \widehat {MPF}\)

\(= {q^2} + {y^2} - 2.q.y.\cos {60^0} \)

\(= {q^2} + {y^2} - qy.\)

nên C đúng.

Đáp án D: \(M{Q^2} = P{M^2} + P{Q^2} = {q^2} + {m^2}\) nên D sai.

Chọn (C).

Loigiaihay.com

Quảng cáo
Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
close