Toán 11, giải toán lớp 11 chân trời sáng tạo

Bài 12 trang 42 SGK Toán 11 tập 1 - Chân trời sáng tạo

Độ sâu h (m) của mực nước ở một cảng biển vào thời điểm t (giờ)

Tổng hợp đề thi học kì 1 lớp 11 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh

Quảng cáo

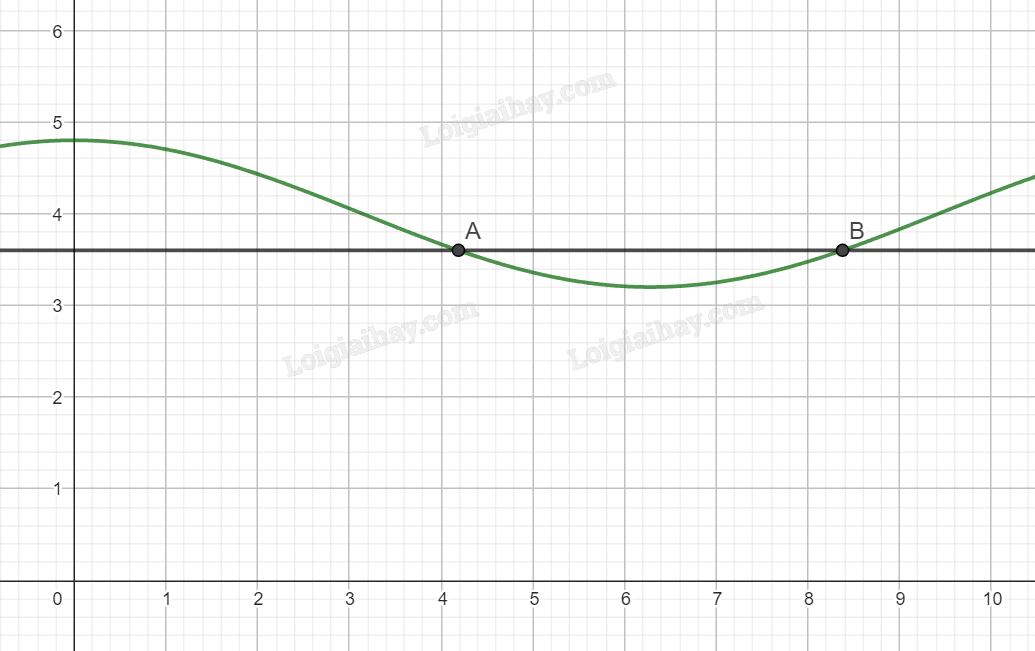
Đề bài

Độ sâu h (m) của mực nước ở một cảng biển vào thời điểm t (giờ) sau khi thuỷ triểu lên lần đầu tiên trong ngày được tính xấp xỉ bởi công thức \(h(t) = 0,8cos0,5t + 4.\)

(Theo https://noc.ac.uk/files/documents/business/an-introduction-to-tidal-modelling.pdf)

a) Độ sâu của nước vào thời điểm t = 2 là bao nhiêu mét?

b) Một con tàu cần mực nước sâu tối thiểu 3,6 m để có thể di chuyển ra vào cảng an toàn. Dựa vào đồ thị của hàm số côsin, hãy cho biết trong vòng 12 tiếng đầu tiên sau khi thuỷ triểu lên lần đầu tiên, ở những thời điểm t nào tàu có thể hạ thuỷ. Làm tròn kết quả đến hàng phần trăm.

Phương pháp giải - Xem chi tiết

a) Thay t = 2 vào công thức h(t).

b) Giải phương trình côsin để tìm t.

Lời giải chi tiết

a) Tại thời điểm t = 2 độ sâu của nước là: \(h\left( 2 \right) = 0,8cos0,5.2 + 4 \approx 4,43{\rm{ }}m.\)

Vậy độ sâu của nước ở thời điểm t = 2 là khoảng 4,43 m.

b) Các thời điểm để mực nước sâu là 3,6m tương ứng với phương trình \(0,8cos0,5t + 4 = 3,6\).

Ta có: \(0,8cos0,5t + 4 = 3,6\)

\(\begin{array}{l} \Leftrightarrow cos0,5t = - \frac{1}{2} = cos\frac{{2\pi }}{3}\\ \Leftrightarrow 0,5t = \pm \frac{{2\pi }}{3} + k2\pi ,k \in \mathbb{Z}\\ \Leftrightarrow t = \pm \frac{{4\pi }}{3} + k4\pi ,k \in \mathbb{Z}\end{array}\)

Với \(t = \frac{{4\pi }}{3} + k4\pi \), trong 12 tiếng ta có các thời điểm \(0 \le \frac{{4\pi }}{3} + k4\pi \le 12 \Leftrightarrow - 0,3 \le k \le 0,62 \Rightarrow k = 0 \Rightarrow t = \frac{{4\pi }}{3}\).

Với \(t = - \frac{{4\pi }}{3} + k4\pi \), trong 12 tiếng ta có các thời điểm \(0 \le - \frac{{4\pi }}{3} + k4\pi \le 12 \Leftrightarrow 0,3 \le k \le 1,28 \Rightarrow k = 1 \Rightarrow t = - \frac{{4\pi }}{3} + 4\pi = \frac{{8\pi }}{3}\).

Hai thời điểm t vừa tìm được chính là giao điểm của đồ thị h(t) với đường thẳng y = 3,6.

Ta thấy trong khoảng \(\left( {\frac{{4\pi }}{3};\frac{{8\pi }}{3}} \right)\), đồ thị h(t) nằm dưới đường thẳng y = 3,6, tức trong khoảng thời gian t đó, mực nước thấp hơn 3,6 m và tàu không thể hạ thủy.

Vậy tàu có thể hạ thủy vào các thời điểm \(t\in \left[ 0;\frac{4\pi }{3} \right]\cup \left[ \frac{8\pi }{3};12 \right]\).