Bài 12 trang 103 Tài liệu dạy – học Toán 9 tập 2

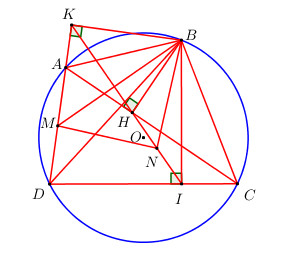
Đề bài

Cho tứ giác ABCD nội tiếp đường tròn (O). Gọi H và I theo thứ tự là hình chiếu của B trên AC, CD. Gọi M và N lần lượt là trung điểm của AD và HI. Chứng minh:

a) Hai tam giác ABD và HBI đồng dạng.

b) \(\widehat {MNB} = {90^o}\).

Lời giải chi tiết

 

a) Xét tứ giác BHIC có : \(\widehat {BHC} = \widehat {BIC} = {90^0}\) (gt) \( \Rightarrow \) 2 điểm H, I cùng nhìn B, C dưới góc 90⁰\( \Rightarrow H;I\) thuộc đường tròn đường kính BC \( \Rightarrow BHIC\) nội tiếp đường tròn đường kính BC.

\( \Rightarrow \widehat {HIB} = \widehat {HCB}\) (hai góc nội tiếp cùng chắn cung HB).

Mà \(\widehat {HCB} = \widehat {ADB}\) (hai góc nội tiếp cùng chắn cung AB của đường tròn \(\left( O \right)\))

\( \Rightarrow \widehat {HIB} = \widehat {ADB}\).

Tương tự ta có : \(\widehat {HBI} = \widehat {HCI}\) (hai góc nội tiếp cùng chắn cung HI của đường tròn đường kính BC).

\(\widehat {HCI} = \widehat {ABD}\)(hai góc nội tiếp cùng chắn cung AD của đường tròn \(\left( O \right)\))

\( \Rightarrow \widehat {HBI} = \widehat {ABD}\)

Xét \(\Delta ABD\) và \(\Delta HBI\) có :

\(\begin{array}{l}\widehat {HIB} = \widehat {ADB}\,\,\left( {cmt} \right);\\\widehat {HBI} = \widehat {ABD}\,\,\left( {cmt} \right);\\ \Rightarrow \Delta ABD \sim \Delta HBI\,\,\left( {g.g} \right)\end{array}\)

b) Gọi K là hình chiếu của B trên AD \( \Rightarrow \widehat {BKD} = {90^0}\).

Xét tứ giác BIDK có : \(\widehat {BID} + \widehat {BKD} = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác BIDK là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 180⁰).

\( \Rightarrow \widehat {DKI} = \widehat {DBI}\) (hai góc nội tiếp cùng chắn cung DI)  (1).

Ta có \(\Delta ABD \sim \Delta HBI\,\,\left( {cmt} \right)\)

\(\Rightarrow \dfrac{{BD}}{{BI}} = \dfrac{{AD}}{{HI}} = \dfrac{{2MD}}{{2NI}} = \dfrac{{MD}}{{NI}}\)

Xét \(\Delta BDM\) và \(\Delta BIN\) có :  

\(\begin{array}{l}\widehat {HIB} = \widehat {ADB}\,\,\left( {cmt} \right);\\\dfrac{{BD}}{{BI}} = \dfrac{{MD}}{{NI}}\,\,\left( {cmt} \right);\end{array}\)

\( \Rightarrow \Delta BDM \sim \Delta BIN\,\,\left( {c.g.c} \right) \)

\(\Rightarrow \widehat {DBM} = \widehat {IBN}\) (2 góc tương ứng)

\( \Rightarrow \widehat {DBM} + \widehat {DBN} = \widehat {IBN} + \widehat {DBN} \)

\(\Rightarrow \widehat {MBN} = \widehat {BDI}\)  (2)

Từ (1) và (2) \( \Rightarrow \widehat {DKI} = \widehat {MBN}\) hay \(\widehat {MKN} = \widehat {MBN} \) (\Rightarrow \) Tứ giác MNBK là tứ giác nội tiếp (Tứ giác có 2 đỉnh cùng nhìn 1 cạnh dưới các góc bằng nhau).

\( \Rightarrow \widehat {BKM} + \widehat {BNM} = {180^0}\) (tổng 2 góc đối của tứ giác nội tiếp)

Mà \(\widehat {BKM} = {90^0}\) (cách dựng) \( \Rightarrow \widehat {BNM} = {90^0}\) (đpcm).

 Loigiaihay.com