Bài 17 trang 103 Tài liệu dạy – học Toán 9 tập 2

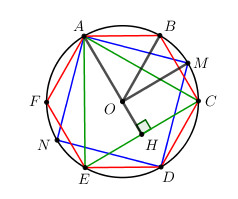
Đề bài

Hãy vẽ các hình lục giác đều, hình vuông, tam giác đều cùng nội tiếp đường tròn (O ; R) rồi tính cạnh của các hình đó theo R.

Lời giải chi tiết

 

+) ABCDEF là lục giác đều \( \Rightarrow \widehat {AOB} = \dfrac{{{{360}^0}}}{6} = {60^0}\).

Xét tam giác OAB có : \(\left\{ \begin{array}{l}OA = OB = R\\\widehat {AOB} = {60^0}\end{array} \right. \Rightarrow \Delta OAB\) đều \( \Rightarrow AB = R\).

Vậy cạnh hình lục giác đều nội tiếp đường tròn \(\left( {O;R} \right)\)là R.

+) AMDN là hình vuông \( \Rightarrow \widehat {AOM} = {90^0} \Rightarrow \Delta OAM\) vuông tại O

\( \Rightarrow O{A^2} + O{M^2} = A{M^2}\) (định lí Pytago)

\({R^2} + {R^2} = A{M^2} \Rightarrow A{M^2} = 2{R^2} \) \(\Leftrightarrow AM = R\sqrt 2 \).

Vậy cạnh hình vuông nội tiếp đường tròn \(\left( {O;R} \right)\)là \(R\sqrt 2 \).

+) ACE là tam giác đều. Gọi H là trung điểm của CE \( \Rightarrow AH \bot CE\) (đường trung tuyến đồng thời là đường cao).

O là tâm đường tròn ngoại tiếp tam giác đều ACE \( \Rightarrow O\) là trọng tâm tam giác ACE \( \Rightarrow AO = \dfrac{2}{3}AH \Rightarrow AH = \dfrac{3}{2}R\).

Xét tam giác vuông ACH có:\(A{H^2} + H{C^2} = A{C^2}\)

\(\Leftrightarrow \dfrac{{9{R^2}}}{4} + {\left( {\dfrac{{AC}}{2}} \right)^2} = A{C^2}\)

\( \Leftrightarrow \dfrac{{9{R^2}}}{4} + \dfrac{{A{C^2}}}{4} = A{C^2} \)

\(\Leftrightarrow \dfrac{{9{R^2}}}{4} = \dfrac{{3A{C^2}}}{4}\)

\(\Leftrightarrow A{C^2} = 3{R^2} \)

\(\Leftrightarrow AC = R\sqrt 3 \).

Vậy cạnh tam giác đều nội tiếp đường tròn \(\left( {O;R} \right)\)là \(R\sqrt 3 \).

 Loigiaihay.com