Bài 21 trang 103 Tài liệu dạy – học Toán 9 tập 2

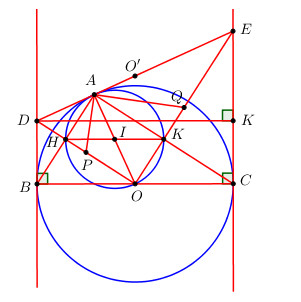
Đề bài

Cho tam giác ABC nội tiếp đường tròn tâm O, bán kính R, đường kính BC với AB < AC. Vẽ đường tròn tâm I, đường kính AO, cắt AB, AC lần lượt tại H và K.

a) Chứng minh H, I, K thẳng hàng.

b) Tia OH và OK lần lượt cắt các tiếp tuyến tại B và C của đường tròn tâm O tại D và E. Chứng minh rằng BD + CE = DE và BD.CE = R².

c) Gọi P,Q lần lượt là trung điểm của OD và OE. Chứng minh tứ giác APOQ nội tiếp.

d) Biết BD = 4 cm, EC = 6 cm. Hãy tính bán kính đường tròn ngoại tiếp tam giác DOE.

Lời giải chi tiết

 

a) Ta có \(\widehat {AHO} = \widehat {AKO} = {90^0}\) (góc nội tiếp chắn nửa đường tròn).

Xét tứ giác AHOK có: \(\widehat {HAK} = \widehat {AHO} = \widehat {AKO} = {90^0} \Rightarrow \) Tứ giác AHOK là hình chữ nhật (Tứ giác có 3 góc vuông).

\( \Rightarrow \) Hai đường chéo AO và HK cắt nhau tại trung điểm đường. Mà I là trung điểm của AO (gt) \( \Rightarrow I\) cũng là trung điểm của HK. Vậy H, I, K thẳng hàng.

b) +) Ta có:

\(\widehat {DAB} = \widehat {AOH}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AH).

\(\widehat {EAC} = \widehat {AOK}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AK).

\( \Rightarrow \widehat {DAB} + \widehat {HAK} + \widehat {EAC}\)\(\, = \widehat {AOH} + \widehat {HAK} + \widehat {AOK} \)\(\,= \widehat {HAK} + \widehat {HOK} = {180^0}\) (tổng hai góc đối của tứ giác nội tiếp) \( \Rightarrow D;A;E\) thẳng hàng.

Áp dụng tính chất 2 tiếp tuyến cắt nhau ta có \(BD = AD;\,\,CE = AE\)

\( \Rightarrow BD + CE = AD + AE\). Mà D; A; E thẳng hàng (cmt) \( \Rightarrow AD + AE = DE\). Vậy \(BD + CE = DE\).

+) Ta có: \(BD.CE = AD.AE\).

Ta có: \(\widehat {DAO} = \widehat {AKO}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AO).

Mà \(\widehat {AKO} = {90^0}\) (AHOK là hình chữ nhật) \( \Rightarrow \widehat {DAO} = {90^0} \Rightarrow AO \bot DE\) tại A.

\(\widehat {HOK} = {90^0}\) (AHOK là hình chữ nhật) \( \Rightarrow \Delta DOE\) vuông tại O.

Áp dụng hệ thức lượng trong tam giác vuông DOE có : \(AD.AE = A{O^2} = {R^2}\).

Vậy BD.CE = R².

c) Xét tam giác vuông OAD có AP là trung tuyến ứng với cạnh huyền OD \( \Rightarrow PA = PO = PD \Rightarrow \Delta PAO\) cân tại P \( \Rightarrow \widehat {POA} = \widehat {PAO}\).

Chứng minh tương tự ta có : \(\widehat {QOA} = \widehat {QAO}\).

\( \Rightarrow \widehat {PAQ} = \widehat {PAO} + \widehat {QAO} \)\(\,= \widehat {POA} + \widehat {QOA} = \widehat {POQ} = {90^0}\).

Xét tứ giác APOQ có: \(\widehat {POQ} + \widehat {PAQ} = {90^0} + 90 = {180^0} \Rightarrow \) Tứ giác APOQ là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 180⁰).

d) Gọi O’ là trung điểm của DE. Vì \(\Delta ODE\) vuông tại O nên O’ là tâm đường tròn ngoại tiếp tam giác DOE và bán kính đường tròn ngoại tiếp tam giác DOE bằng \(\dfrac{{DE}}{2}\).

Mà \(DE = BD + CE = 4 + 6 = 10\,\,\left( {cm} \right)\)

\(\Rightarrow R = \dfrac{{DE}}{2} = 5\,\,\left( {cm} \right)\).

 Loigiaihay.com