Bài 11 trang 71 SGK Hình học 10 nâng caoCho hai đường tròn Quảng cáo
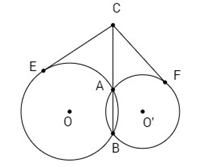
Đề bài Cho hai đường tròn \((O\,;\,R)\) và \(({O'}\,;\,{R'})\) cắt nhau tại hai điểm A và B. Trên đường thẳng AB, lấy điểm C ở ngoài hai đường tròn và kẻ hai tiếp tuyến CE, CF đến hai đường tròn đó ( E, F là các tiếp điểm). Chứng minh rằng CE = CF. Lời giải chi tiết Ta có \(\eqalign{ Chú ý: Hai công thức ở trên là sử dụng công thức trang 50 SGK Hình học 10 nâng cao. Các em cũng có thể chứng minh chi tiết như sau: Áp dụng công thức phương tích của điểm C với hai đường tròn ta có:
*Do CE là tiếp tuyến của (O) nên tam giác CEO vuông tại E.
* Do CF là tiếp tuyến của (O’) nên tam giác CFO’ vuông tại F.
Loigiaihay.com
|














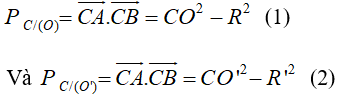
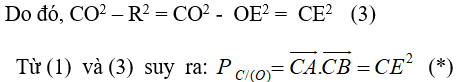
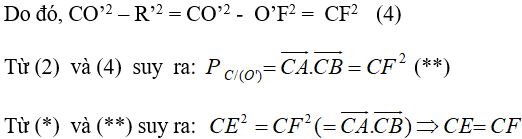






Danh sách bình luận