Bài 12 trang 71 SGK Hình học 10 nâng caoCho đường tròn (O; R) và một điểm P cố định ở bên trong đường tròn đó. Hai dây cung thay đổi AB và CD luôn đi qua P và vuông góc với nhau. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
Cho đường tròn (O; R) và một điểm P cố định ở bên trong đường tròn đó. Hai dây cung thay đổi AB và CD luôn đi qua P và vuông góc với nhau. LG a Chứng minh rằng \(A{B^2} + C{D^2}\) không đổi. Lời giải chi tiết:
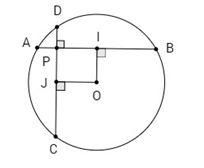
Gọi I và J theo thứ tự là trung điểm của AB và CD. Theo định lí quan hệ giữa đường kính và dây ta có: OI ⊥ AB; OJ ⊥ CD; Do đó tứ giác OIPJ là hình chữ nhật. Ta có: AB2 + CD2 = (2AI)2 + (2DJ)2 = 4 AI2 + 4DJ2 = 4. (AO2 – OI2 ) + 4(DO2 – OJ2 ) =4. (R2 – OI2 ) + 4(R2 – OJ2 ) = 4( 2R2 – OI2 – OJ2 ) = 4.[2R2 – (OI2 + OJ2) ] = 4. ( 2R2 – OP2) ( vì OI2 + OJ2 = OI2 + IP2 = OP2 ) = 8R2 – 4. OP2 (không đổi vì R không đổi, O và P cố định nên OP không đổi) LG b Chứng minh rằng \(P{A^2} + P{B^2} + P{C^2} + P{D^2}\) không phụ thuộc vào vị trí của điểm P. Lời giải chi tiết: Phương tích của điểm P với đường tròn: \(\begin{array}{l}{P_{P/\left( O \right)}} = \overrightarrow {PA} .\overrightarrow {PB} = O{P^2} - {R^2}\\{P_{P/\left( O \right)}} = \overrightarrow {PC} .\overrightarrow {PD} = O{P^2} - {R^2}\end{array}\) Ta có \(\eqalign{ Vậy \(P{A^2} + P{B^2} + P{C^2} + P{D^2}\) không phụ thuộc vào vị trí của điểm P. Loigiaihay.com
|




















Danh sách bình luận