Bài 1 trang 54 SBT Hình học 12 Nâng caoGiải bài 1 trang 54 sách bài tập Hình học 12 Nâng cao. Cho tứ diện ABCD, biết AB=BC=AC=BD=a, AD=b, ... Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
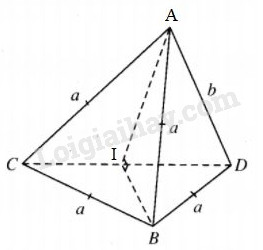
Cho tứ diện ABCD, biết AB=BC=AC=BD=a, AD=b, hai mặt phẳng (ACD) và (BCD) vuông góc với nhau. LG a Chứng minh rằng tam giác ACD vuông. Lời giải chi tiết:
Gọi \(I\) là trung điểm của CD, do BC = BD = a nên \(BI \bot CD.\) Mặt khác \(mp\left( {BCD} \right) \bot mp\left( {ACD} \right)\) nên \(BI \bot mp(ACD).\) Xét các tam giác vuông AIB và DIB có cạnh góc vuông BI chung, BA = BD, từ đó AI = ID. Vậy ACD là tam giác vuông tại A. LG b Tính diện tích mặt cầu ngoại tiếp tứ diện ABCD. Lời giải chi tiết:
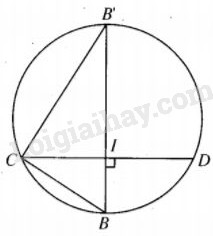
Từ chứng minh trên, ta thấy tâm của mặt cầu ngoại tiếp tứ diện ABCD thuộc BI, do đó, bán kính mặt cầu phải tìm chính là bán kính R của đường tròn ngoại tiếp tam giác BCD. Dễ thấy CB2=BI.BB’=2R.BI, tức là \(R = {{{a^2}} \over {2BI}}.\) Mặt khác \(\eqalign{ & B{I^2} = B{C^2} - {{C{D^2}} \over 4} = {a^2} - {{{a^2} + {b^2}} \over 4} = {{3{a^2} - {b^2}} \over 4} \cr & \Rightarrow BI = {1 \over 2}\sqrt {3{a^2} - {b^2}} ,0 < b < a\sqrt 3 . \cr} \) Như vậy \(R = {{{a^2}} \over {\sqrt {3{a^2} - {b^2}} }}\) Do đó diện tích mặt cầu phải tìm bằng \({{4\pi {a^4}} \over {3{a^2} - {b^2}}}\) với \(0 < b < a\sqrt 3 \). Loigiaihay.com
|




















Danh sách bình luận