Bài 6 trang 54 SBT Hình học 12 Nâng cao

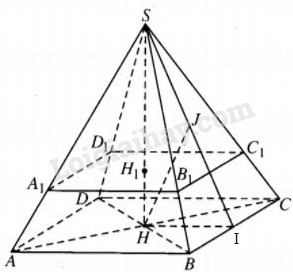
LG a

Chứng minh rằng tồn tại mặt cầu tâm H tiếp xúc với tất cả các mặt bên của hình chóp. Tính bán kính R của mặt cầu đó.

Lời giải chi tiết:

Gọi I là trung điểm của BC thì \(HI = {a \over 2} = SH.\)

Gọi J là trung điểm của SI thì \(HJ \bot SI,\) mặt khác \(HJ \bot BC\), vậy \(HJ \bot mp(SBC)\) đồng thời \(HJ = {{SI} \over 2} = {1 \over 2}.{a \over 2}\sqrt 2  = {{a\sqrt 2 } \over 4}.\)

Tương tự, ta có khoảng cách từ H tới các mặt bên của hình chóp đã cho cũng bằng \({{a\sqrt 2 } \over 4}.\)

Như vậy, mặt cầu tiếp xúc với các mặt bên của hình chóp S.ABCD.

LG b

Gọi (P) là mặt phẳng song song với mp(ABCD) và cách mp(ABCD) một khoảng x (0 < x < R). Gọi S_td là diện tích thiết diện tạo bởi mp(P) và hình chóp bỏ đi phần nằm trong mặt cầu. Hãy xác định x để \({S_{td}} = \pi {R^2}.\)

Lời giải chi tiết:

Gọi H₁ là giao điểm của (P) và SH thì \(H{H_1} = x,0 < H{H_1} < R\) và thiết diện của hình chóp với (P) là hình vuông \({A_1}{B_1}{C_1}{D_1}.\) Khi ấy

\({{{S_{{A_1}{B_1}{C_1}{D_1}}}} \over {{S_{ABCD}}}} = {\left( {{{{a \over 2} - x} \over {{a \over 2}}}} \right)^2} = {{{{\left( {a - 2x} \right)}^2}} \over {{a^2}}}.\)

Từ đó \({S_{{A_1}{B_1}{C_1}{D_1}}} = {(a - 2x)^2}.\)

Ta có (P) cắt mặt cầu nêu trên theo đường tròn bán kính r được tính bởi \({r^2} = {R^2} - {x^2}\) hay \({r^2} = {{{a^2}} \over 8} - {x^2} = {{{a^2} - 8{x^2}} \over 8},\) từ đó diện tích hình tròn thu được là \({1 \over 8}\pi \left( {{a^2} - 8{x^2}} \right).\)Vậy

\(\eqalign{   {S_{td}} &= {(a - 2x)^2} - {1 \over 8}\pi ({a^2} - 8{x^2}) \cr&= {1 \over 8}\left[ {8{{(a - 2x)}^2} - \pi ({a^2} - 8{x^2})} \right].  \cr  &  \cr} \)

Ta có

\(\eqalign{  & {S_{td}} = \pi {R^2} = {1 \over 8}\pi {a^2} \cr&\Leftrightarrow 8{(a - 2x)^2} - \pi {a^2} + 8\pi {x^2} = \pi {a^2}  \cr  &  \Leftrightarrow 4\left[ {{{(a - 2x)}^2} + \pi {x^2}} \right] = \pi {a^2}  \cr  &  \Leftrightarrow x = {{4a - \pi a} \over {8 + 2\pi }} \cr} \)

(vì \(0 < x < R = {{a\sqrt 2 } \over 4}\)).

Loigiaihay.com