Lý thuyết Phương trình mặt phẳng Toán 12 Cùng khám phá1. Vecto pháp tuyến và cặp vecto chỉ phương của mặt phẳng Vecto pháp tuyến Quảng cáo
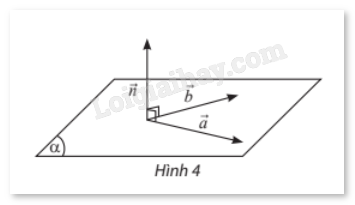
1. Vecto pháp tuyến và cặp vecto chỉ phương của mặt phẳng Vecto pháp tuyến
Cặp vecto chỉ phương
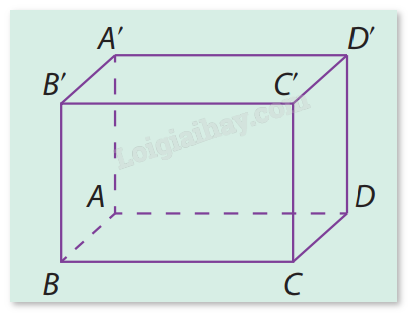
Ví dụ: Cho hình hộp chữ nhật ABCD.A’B’C’D’. Hãy tìm bốn vecto pháp tuyến và hai cặp vecto chỉ phương của mặt phẳng (AA’B’B).
Giải: Bốn vecto pháp tuyến của mặt phẳng (AA’B’B) là: \(\overrightarrow {AD} \), \(\overrightarrow {A'D'} \), \(\overrightarrow {BC} \), \(\overrightarrow {B'C'} \). Hai cặp vecto chỉ phương của mặt phẳng (AA’B’B) là: \(\overrightarrow {AB} \), \(\overrightarrow {AA'} \) và \(\overrightarrow {AB} \), \(\overrightarrow {AB'} \). Xác định vecto pháp tuyến của mặt phẳng khi biết cặp vecto chỉ phương
Vecto \(\overrightarrow n = ({a_2}{b_3} - {a_3}{b_2};{a_3}{b_1} - {a_1}{b_3};{a_1}{b_2} - {a_2}{b_1})\) còn được gọi là tích có hướng của hai vecto \(\overrightarrow a = ({a_1};{a_2};{a_3})\) và \(\overrightarrow b = ({b_1};{b_2};{b_3})\), kí hiệu là \(\left[ {\overrightarrow a ,\overrightarrow b } \right]\). Biểu thức \({a_1}{b_2} - {a_2}{b_1}\) thường được kí hiệu là \(\left| {\begin{array}{*{20}{c}}{{a_1}}&{{a_2}}\\{{b_1}}&{{b_2}}\end{array}} \right|\). Nếu \(\overrightarrow a ,\overrightarrow b \) cùng phương \( \Leftrightarrow \left[ {\overrightarrow a ,\overrightarrow b } \right] = 0\). Ví dụ: Cho mặt phẳng (P) nhận \(\overrightarrow a = (1;2;3)\), \(\overrightarrow b = (4;1;5)\) làm cặp vecto chỉ phương. Tìm một vecto pháp tuyến của (P). Giải: Ta có tích có hướng của hai vecto \(\overrightarrow a \), \(\overrightarrow b \) là \(\left[ {\overrightarrow a ,\overrightarrow b } \right] = (2.5 - 3.1;3.4 - 1.5;1.1 - 2.4) = (7;7; - 7)\). Do đó, mặt phẳng (P) nhận \(\overrightarrow n = \frac{1}{7}\left[ {\overrightarrow a ,\overrightarrow b } \right] = (1;1; - 1)\) làm một vecto pháp tuyến. 2. Phương trình tổng quát của mặt phẳng Định nghĩa
Mỗi phương trình Ax + By + Cz + D = 0 (A, B, C không đồng thời bằng 0) đều xác định một mặt phẳng nhận \(\overrightarrow n = (A;B;C)\) làm vecto pháp tuyến. Cho mặt phẳng có phương trình tổng quát là Ax + By + Cz + D = 0 . Khi đó \(N({x_0};{y_0};{z_0}) \in (\alpha ) \Leftrightarrow A{x_0} + B{y_0} + C{z_0} + D = 0\). Ví dụ: Cho hai mặt phẳng (P), (Q) có phương trình tổng quát là (P): \(3x - 5y + 7z = 0\) và (Q): \(x + y - 2 = 0\). a) Tìm một vecto pháp tuyến của mỗi mặt phẳng (P), (Q). b) Tìm điểm thuộc mặt phẳng (P) trong số các điểm A(1;3;1), B(1;2;3). Giải: a) Mặt phẳng (P) có một vecto pháp tuyến là \(\overrightarrow n = (3; - 5;7)\). Mặt phẳng (Q) có một vecto pháp tuyến là \(\overrightarrow n = (1;1;0)\). b) Thay tọa độ điểm A vào phương trình của (P), ta được: 3.1 – 5.3 + 7.1 + 5 = 0. Vậy A thuộc (P). Thay tọa độ điểm B vào phương trình của (P), ta được: 3.1 – 5.2 + 7.3 + 5 = 19 \( \ne 0\). Vậy B không thuộc (P). Lập phương trình tổng quát của mặt phẳng đi qua một điểm và biết vecto pháp tuyến
Ví dụ: Viết phương trình mặt phẳng (P) đi qua điểm M(1;2;3) và có vecto pháp tuyến \(\overrightarrow n = (1;2;1)\). Giải: Vì (P) đi qua điểm M(1;2;1) và có vecto pháp tuyến \(\overrightarrow n = (1;2;1)\) nên phương trình của (P) là \(1\left( {x-1} \right) + 2\left( {y-2} \right) + 1\left( {z-3} \right) = 0 \Leftrightarrow x + 2y - 8 = 0\). Lập phương trình mặt phẳng đi qua một điểm và biết cặp vecto chỉ phương
Ví dụ: Viết phương trình mặt phẳng (P) đi qua điểm N(4;0;1) và có cặp vecto chỉ phương là \(\overrightarrow a = (1;2;1)\), \(\overrightarrow b = (2;1;3)\). Giải: (P) có cặp vecto chỉ phương là \(\overrightarrow a = (1;2;1)\), \(\overrightarrow b = (2;1;3)\), suy ra (P) có vecto pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow a ,\overrightarrow b } \right] = (2.3 - 1.1;1.2 - 1.3;1.1 - 2.2) = (5; - 1; - 3)\). Phương trình của (P) là \(5(x - 4) - 1(y - 0) - 3(z - 1) = 0 \Leftrightarrow 5x - y - 3z - 17 = 0\). Lập phương trình mặt phẳng đi qua ba điểm không thẳng hàng
Ví dụ: Viết phương trình mặt phẳng (P) đi qua ba điểm A(1;1;1), B(1;2;2), C(4;1;0). Giải: (P) đi qua ba điểm A(1;1;1), B(1;2;2), C(4;1;0) nên có cặp vecto chỉ phương là \(\overrightarrow {AB} = (0;1;1)\), \(\overrightarrow {AC} = (3;0; - 1)\), suy ra (P) có vecto pháp tuyến là \(\overrightarrow n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = (1.( - 1) - 1.0;1.3 - 0.( - 1);0.0 - 1.3) = ( - 1;3; - 3)\). Phương trình của (P) là \( - 1(x - 1) + 3(y - 1) - 3(z - 1) = 0 \Leftrightarrow x - 3y + 3z = 0\). Phương trình mặt phẳng theo đoạn chắn
3. Điều kiện để hai mặt phẳng song song, vuông góc Trong không gian Oxyz, cho hai mặt phẳng: \(\left( {{\alpha _1}} \right):{A_1}x + {B_1}y + {C_1}z + {D_1} = 0\), \(\left( {{\alpha _2}} \right):{A_2}x + {B_2}y + {C_2}z + {D_2} = 0\) với hai vecto pháp tuyến \(\overrightarrow {{n_1}} = ({A_1};{B_1};{C_1})\), \(\overrightarrow {{n_2}} = ({A_2};{B_2};{C_2})\) tương ứng. Giả sử điểm \(M \in ({\alpha _1})\). Điều kiện để hai mặt phẳng song song
Điều kiện để hai mặt phẳng trùng nhau
Ví dụ: Trong không gian Oxyz, cho mặt phẳng (P): \(2x - 3y + z + 5 = 0\). a) Chứng minh rằng mặt phẳng (Q): \( - 4x + 6y - 2z + 7 = 0\) song song với (P). b) Viết phương trình mặt phẳng (P’) đi qua điểm M(1;-2;3) và song song với (P). Giải: a) Xét (P): \(2x - 3y + z + 5 = 0\) và (Q): \( - 4x + 6y - 2z + 7 = 0\). Ta có \(\frac{2}{{ - 4}} = \frac{{ - 3}}{6} = \frac{1}{{ - 2}} \ne \frac{5}{7}\) nên (P)//(Q). b) Mặt phẳng (P) có vecto pháp tuyến \(\overrightarrow n = (2; - 3;1)\). Vì (P’)//(P) nên (P’) có vecto pháp tuyến \(\overrightarrow n = (2; - 3;1)\). Vậy mặt phẳng (P’) đi qua đi qua M(1;-2;3) và có vecto pháp tuyến \(\overrightarrow n = (2; - 3;1)\) có phương trình là: \(2(x - 1) - 3(y + 2) + 1(z - 3) = 0\) hay \(2x - 3y + z - 11 = 0\). Điều kiện để hai mặt phẳng cắt nhau
Điều kiện để hai mặt phẳng vuông góc
Ví dụ: Cho ba mặt phẳng (P), (Q), (R) có phương trình là (P): \(x - 4y + 3z + 2 = 0\), (Q): \(4x + y + 88 = 0\), (R): \(x + y + z + 9 = 0\). Chứng minh rằng (P) ⊥ (Q), (P) ⊥ (R). Giải: Các mặt phẳng (P), (Q), (R) có vecto pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = (1; - 4;3)\), \(\overrightarrow {{n_2}} = (4;1;0)\), \(\overrightarrow {{n_3}} = (1;1;1)\). Ta có \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 1.4 + ( - 4).1 + 3.0 = 0\). Vậy (P) ⊥ (Q). Ta có \(\overrightarrow {{n_1}} .\overrightarrow {{n_3}} = 1.1 + ( - 4).1 + 3.1 = 0\). Vậy (P) ⊥ (R). 4. Khoảng cách từ một điểm đến một mặt phẳng
Ví dụ 1: Tìm khoảng cách từ điểm M(1;2;3) đến mặt phẳng (P): \(x + y + z + 12 = 0\). Giải: \(d\left( {M,(P)} \right) = \frac{{\left| {1.1 + 1.2 + 1.3 + 12} \right|}}{{\sqrt {{1^2} + {1^2} + {1^2}} }} = \frac{{18}}{{\sqrt 3 }} = 6\sqrt 3 \). Ví dụ 2: Chứng minh \((\alpha )\): 2x + 3y – 6z – 7 = 0 song song với \((\beta )\): 2x + 3y – 6z + 14 = 0 và tìm khoảng cách giữa chúng. Giải: Ta có \(\frac{2}{2} = \frac{3}{3} = \frac{{ - 6}}{{ - 6}} \ne \frac{{ - 7}}{{14}}\) nên \((\alpha )\)//\((\beta )\). Lấy điểm N(-7;0;0) thuộc \((\beta )\). Vậy \(d\left( {(\alpha ),(\beta )} \right) = d\left( {N,(\alpha )} \right) = \frac{{\left| {2.( - 7) + 3.0 - 6.3 - 7} \right|}}{{\sqrt {{2^2} + {3^2} + {{( - 6)}^2}} }} = \frac{{21}}{7} = 3\).
|




















Danh sách bình luận