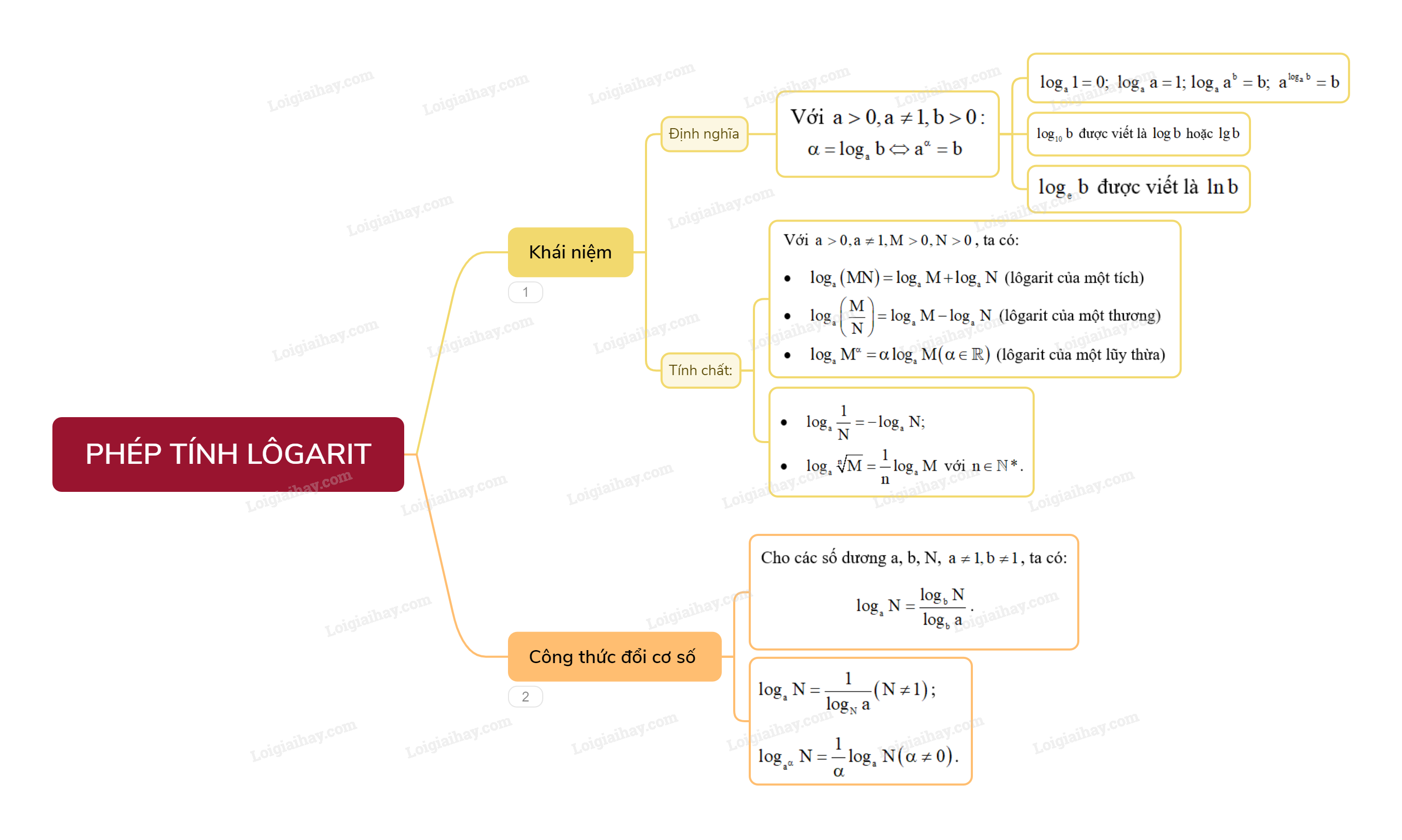
Lý thuyết Phép tính lôgarit - Toán 11 Chân trời sáng tạo1. Khái niệm lôgarit Cho hai số thực dương a, b với (a ne 1). Số thực (alpha ) thỏa mãn đẳng thức ({a^alpha } = b) được gọi là lôgarit cơ số a của b và kí hiệu là ({log _a}b). Quảng cáo
1. Khái niệm lôgarit Cho hai số thực dương a, b với \(a \ne 1\). Số thực \(\alpha \) thỏa mãn đẳng thức \({a^\alpha } = b\) được gọi là lôgarit cơ số a của b và kí hiệu là \({\log _a}b\). \(\alpha = {\log _a}b \Leftrightarrow {a^\alpha } = b\). Chú ý: Từ định nghĩa, ta có:
2. Tính chất Với \(a > 0,a \ne 1,M > 0,N > 0\), ta có:
Chú ý: Đặc biệt, ta có:
3. Công thức đổi cơ số Cho các số dương a, b, N, \(a \ne 1,b \ne 1\), ta có: \({\log _a}N = \frac{{{{\log }_b}N}}{{{{\log }_b}a}}\). Đặc biệt, ta có: \({\log _a}N = \frac{1}{{{{\log }_N}a}}\left( {N \ne 1} \right)\); \({\log _{{a^\alpha }}}N = \frac{1}{\alpha }{\log _a}N\left( {\alpha \ne 0} \right)\).
|




















Danh sách bình luận