Lý thuyết hình vuôngHình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau. Quảng cáo
I. Các kiến thức cần nhớ Định nghĩa: Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau. 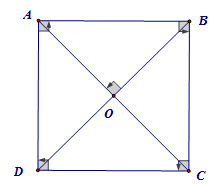 Nhận xét 1: + Hình vuông là hình chữ nhật có bốn cạnh bằng nhau. + Hình vuông là hình thoi có một góc vuông. Như vậy, hình vuông vừa là hình chữ nhật, vừa là hình thoi. Tính chất: + Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi. + Đường chéo của hình vuông vừa bằng nhau vừa vuông góc với nhau Dấu hiệu nhận biết: + Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông. + Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông + Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông + Hình thoi có một góc vuông là hình vuông + Hình thoi có hai đường chéo bằng nhau là hình vuông Nhận xét 2: Một tứ giác vừa là hình chữ nhật, vừa là hình thoi thì tứ giác đó là hình vuông. II. Các dạng toán thường gặp Dạng 1: Vận dụng dấu hiệu nhận biết để chứng minh một tứ giác là hình vuông. Phương pháp: Ta sử dụng các dấu hiệu nhận biết: + Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông. + Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông + Hình chữ nhật có một đường chéo là đường phân giác của một góc là hình vuông + Hình thoi có một góc vuông là hình vuông + Hình thoi có hai đường chéo bằng nhau là hình vuông Dạng 2: Vận dụng kiến thức về hình vuông để chứng minh và giải các bài toán cơ bản: chứng minh một tứ giác là hình vuông,tìm thêm điều kiện của đề bài để một tứ giác là hình vuông, tính độ dài… Phương pháp: Ta sử dụng định nghĩa và các tính chất của hình vuông. + Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau. + Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi. + Đường chéo của hình vuông vừa bằng nhau vừa vuông góc với nhau
|




















Danh sách bình luận