Bài 79 trang 108 SGK Toán 8 tập 1Một hình vuông có cạnh bằng 3cm. Đường chéo của hình vuông đó bằng Quảng cáo
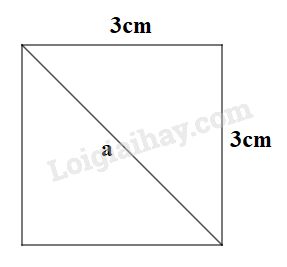
Video hướng dẫn giải LG a. Một hình vuông có cạnh bằng \(3cm\). Đường chéo của hình vuông đó bằng \(6cm\), \(\sqrt{18}cm\), \(5cm\) hay \(4cm\) ? Phương pháp giải: Áp dụng định lí Pytago: Bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông. Lời giải chi tiết: Gọi đường chéo của hình vuông có độ dài là \(a\).
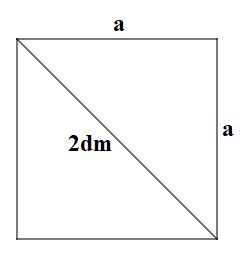
Ta có: \({a^{2}} = {\rm{ }}{3^2} + {\rm{ }}{3^2} = {\rm{ }}18\) (định lí Pytago) Suy ra \(a = \sqrt{18}\) (cm) Vậy đường chéo của hình vuông cạnh \(3\,cm\) là \(\sqrt{18}cm\). LG b. Đường chéo của một hình vuông bằng \(2dm\). Cạnh của hình vuông đó bằng: \(1dm, \dfrac{3}{2}dm\), \(\sqrt{2}dm\) hay \(\dfrac{4}{3}dm\) ? Phương pháp giải: Áp dụng định lí Pytago: Bình phương cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông. Lời giải chi tiết: Gọi cạnh của hình vuông là \(a\).
Áp dụng định lí Pytago ta có: Ta có \({a^2} + {a^2} = {2^2} \Rightarrow 2{a^2} = 4 \Rightarrow {a^2} = 2\)\( \Rightarrow a = \sqrt{2}\) Vậy cạnh của hình vuông có đường chéo \(2\,dm\) là \(\sqrt{2}dm\). Loigiaihay.com
|




















Danh sách bình luận