Lý thuyết Các phép toán với đa thức nhiều biến SGK Toán 8 - Chân trời sáng tạo

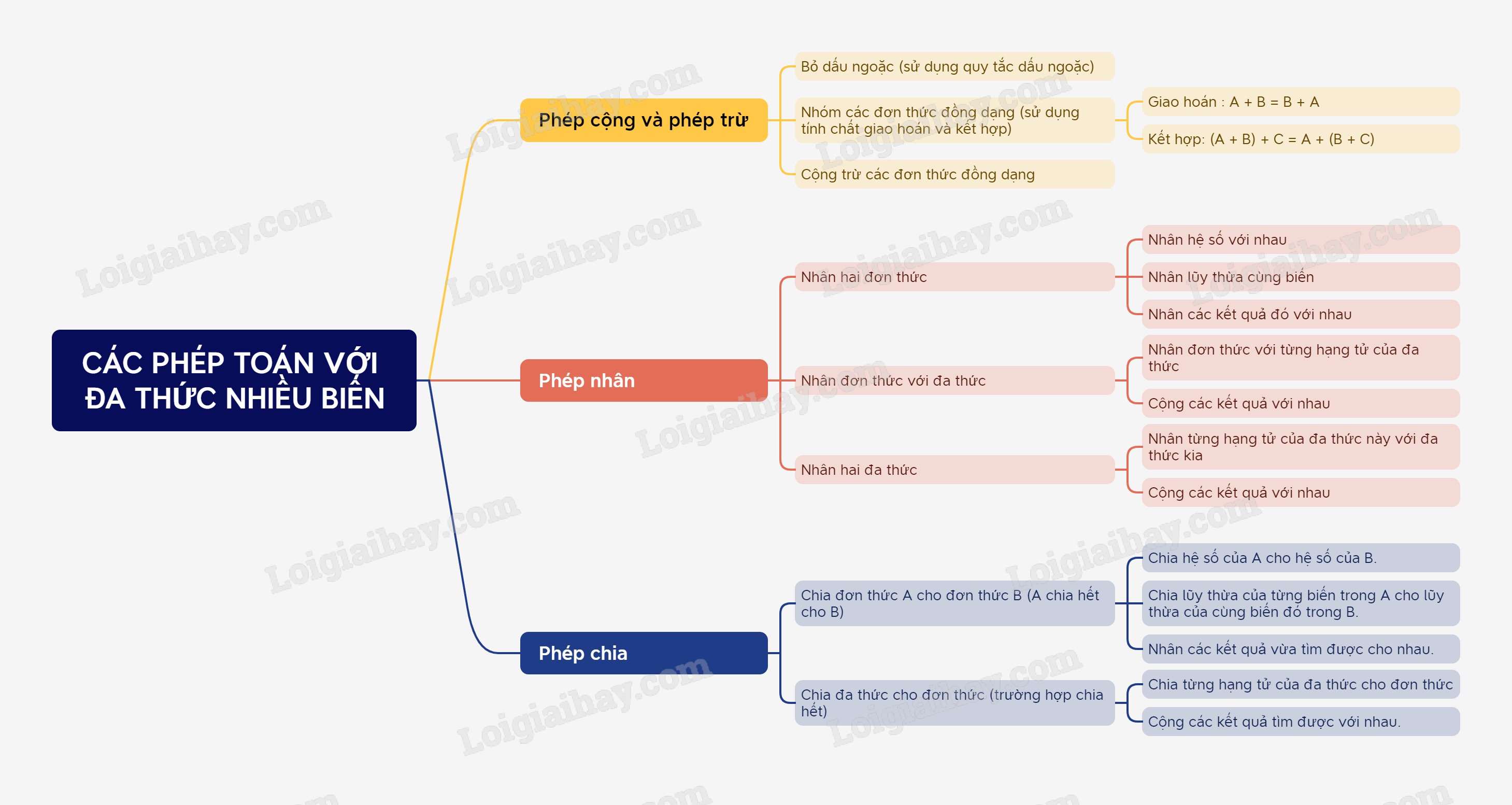
1. Cộng và trừ hai đa thức 

Để cộng, trừ hai đa thức ta thực hiện các bước:

- Bỏ dấu ngoặc (sử dụng quy tắc dấu ngoặc);

- Nhóm các đơn thức đồng dạng (sử dụng tính chất giao hoán và kết hợp);

- Cộng, trừ các đơn thức đồng dạng

Ví dụ:

Cho hai đa thức \(A = 3{x^2} - xy\)và \(B = {x^2} + 2xy - {y^2}\)

\(\begin{array}{l}A + B = \left( {3{x^2} - xy} \right) + \left( {{x^2} + 2xy - {y^2}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^2} - xy + {x^2} + 2xy - {y^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = (3{x^2} + {x^2}) + ( - xy + 2xy) - {y^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 4{x^2} + xy - {y^2}\end{array}\)

\(\begin{array}{l}A - B = \left( {3{x^2} - xy} \right) - \left( {{x^2} + 2xy - {y^2}} \right)\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 3{x^2} - xy - {x^2} - 2xy + {y^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = (3{x^2} - {x^2}) + ( - xy - 2xy) + {y^2}\\\,\,\,\,\,\,\,\,\,\,\,\,\, = 2{x^2} - 3xy + {y^2}\end{array}\)

2. Nhân hai đơn thức 

Để nhân hai đơn thức, ta nhân các hệ số với nhau, nhân các lũy thừa cùng biến, rồi nhân các kết quả đó với nhau.

Ví dụ: \(( - 3{x^2}y)(4xy) = \left[ {\left( { - 3.4} \right)} \right].({x^2}.x).\left( {y.y} \right) =  - 12.{x^3}.{y^2}\)

3. Nhân đơn thức với đa thức  

Để nhân đơn thức với đa thức, ta nhân đơn thức đó với từng hạng tử của đa thức, rồi cộng các kết quả với nhau.

Ví dụ:

\(\begin{array}{l}3{x^2}y\left( {2{x^2}y - xy + 3{y^2}} \right)\\ = (3{x^2}y).(2{x^2}y) - (3{x^2}y).(xy) + (3{x^2}y).(3{y^2})\\ = 3.2.({x^2}.{x^2})\left( {y.y} \right) - 3.({x^2}.x).\left( {y.y} \right) + 3.3.{x^2}.\left( {y.{y^2}} \right)\\ = 6{x^4}{y^2} - 3{x^3}.{y^2} + 9{x^2}{y^3}\end{array}\)

4. Nhân hai đa thức 

Để nhân hai đa thức, ta nhân từng hạng tử của đa thức này với đa thức kia, rồi cộng các kết quả với nhau.

Ví dụ:

\(\begin{array}{l}(xy + 1)(xy - 3)\\ = (xy).\left( {xy} \right) + xy - 3xy - 3\\ = {x^2}{y^2} - 2xy - 3\end{array}\)

5. Chia đơn thức cho đơn thức 

Muốn chia đơn thức A cho đơn thức B (với A chia hết cho B), ta làm như sau:

- Chia hệ số của A cho hệ số của B.

- Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.

- Nhân các kết quả vừa tìm được cho nhau.

Ví dụ:

 \(\begin{array}{l}16{x^4}{y^3}:( - 8{x^3}{y^2})\\ = (16:( - 8)).({x^4}:{x^3}).\left( {{y^3}:{y^2}} \right)\\ =  - 2xy\end{array}\)

6. Chia đa thức cho đơn thức

Muốn chia một đa thức cho một đơn thức (trường hợp chia hết), ta chia từng hạng tử của đa thức cho đơn thức đó, rồi cộng các kết quả tìm được với nhau.

Ví dụ:

\(\begin{array}{l}({x^2}y + {y^2}x):xy\\ = {x^2}y:xy + {y^2}x:xy\\ = x + y\end{array}\)