Hoạt động 23 trang 125 Tài liệu dạy – học Toán 8 tập 1Giải bài tập Cho hình 43, trong đó các đường thẳng a, b, c, d song song với nhau. Quảng cáo
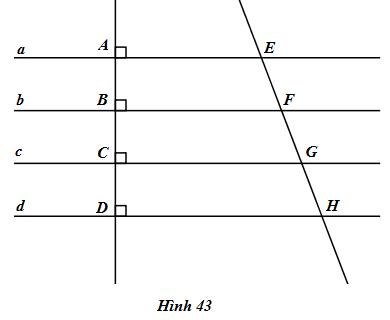
Đề bài Cho hình 43, trong đó các đường thẳng a, b, c, d song song với nhau. Chứng minh rằng: a) Nếu các đường thẳng a, b, c, d song song và cách đều thì EF = FG = GH. b) Nếu EF = FG = GH thì các đường thẳng a, b, c, d song song và cách đều nhau.
Lời giải chi tiết a) Hình thang AEGC (AE //GC) có: \(\left. \matrix{ AB = BC \hfill \cr BF//AE//CG \hfill \cr} \right\} \Rightarrow EF = FG\) Hình thang BFHD (BF // DH) có: \(\left. \matrix{ BC = CD \hfill \cr CG//BF//DH \hfill \cr} \right\} \Rightarrow FG = GH\) Vậy EF = FG = GH b) Hình thang AEGC có: \(\left. \matrix{ EF = FG \hfill \cr BF//AE//CG \hfill \cr} \right\} \Rightarrow AB = BC\) Hình thang BFHD (BF // HD) có: \(\left. \matrix{ FG = GH \hfill \cr CG//BF//DH \hfill \cr} \right\} \Rightarrow BC = CD\) Ta có AB = BC = CD. Do đó a, b, c, d là các đường thẳng song song và cách đều. Loigiaihay.com  Chia sẻ Bình luận
Quảng cáo
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
