Phần câu hỏi bài 2 trang 135, 136 Vở bài tập toán 9 tập 2

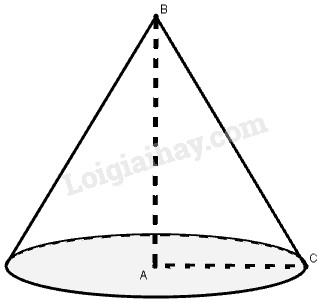
Câu 4

Khi quay hình tam giác vuông \(ABC\) một vòng quanh cạnh góc vuông \(AB\) cố định, ta được một hình nón. Biết rằng \(AB = 4cm; AC = 3cm\). Diện tích xung quanh của hình nón đó bằng:

(A) \(12\pi \,\,c{m^2}\)                   (B) \(15\pi \,\,c{m^2}\)

(C) \(16\pi \,\,c{m^2}\)                   (D) \(20\pi \,\,c{m^2}\)

Khoanh tròn vào chữ cái trước kết quả đúng.

Phương pháp giải:

Tính \(BC\) dựa vào định lý Pytago

Diện tích xung quanh của hình nón có bán kính đáy \(r\) và đường sinh \(l\) là \({S_{xq}} = \pi rl\)

Lời giải chi tiết:

Vì tam giác \(ABC\) vuông tại \(A\) nên theo định lý Pytago ta có \(BC = \sqrt {A{B^2} + A{C^2}}  = \sqrt {{4^2} + {3^2}}\)\(  = \sqrt {25}  = 5cm\)

Khi quay  tam giác vuông \(ABC\) quanh cạnh \(AB\) ta được hình nón có chiều cao \(AB\), bán kính đáy \(AC\) và đường sinh \(BC\) nên diện tích xung quanh của hình nón là \({S_{xq}} = \pi rl = \pi .AC.BC = \pi .3.5 \)\(= 15\pi \left( {c{m^2}} \right)\)

Chọn B.

Câu 5

Một hình nó có đường sinh l = 20cm, diện tích xung quanh  \({S_{xq}} = {\rm{ }}753,6{\rm{ }}c{m^2}\) . Khi đó, bán kính đáy của hình nón bằng  (lấy \(\pi  = 3,14\))

 (A) 9 cm                                 (B) 12 cm

(C) 14 cm                                (D) 15 cm

Khoanh tròn vào chữ cái trước kết quả đúng.

Phương pháp giải:

Diện tích xung quanh của hình nón có bán kính đáy \(r\) và đường sinh \(l\) là \({S_{xq}} = \pi rl\) , từ đó ta tính bán kính đáy \(r.\)

Lời giải chi tiết:

Gọi \(r\left( {r > 0} \right)\) là bán kính đáy của hình nón.

Ta có diện tích xung quanh \({S_{xq}} = \pi rl \Leftrightarrow \pi .r.20 = 753,6 \)\(\Leftrightarrow r = 12cm.\)

Chọn B.

Loigiaihay.com