Bài 10 trang 137 Vở bài tập toán 9 tập 2

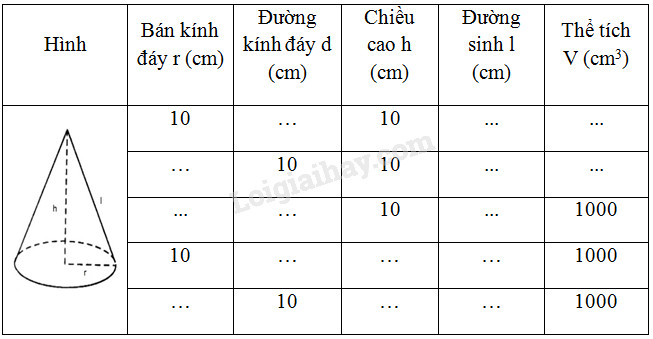
Đề bài

Hãy điền đủ vào các ô trống (…) ở bảng sau:

Lời giải chi tiết

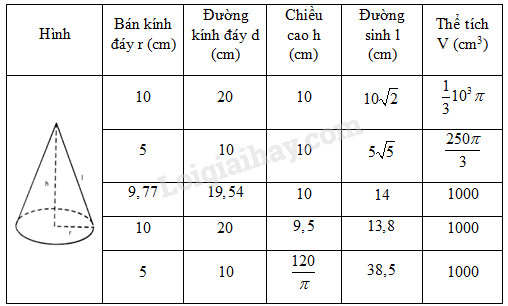
 + Khi \(r = 10cm\) và \(h = 10cm\) ta có đường kính \(d = 2r = 20\left( {cm} \right)\)

- Đường sinh \(l = \sqrt {{r^2} + {h^2}}  = \sqrt {{{10}^2} + {{10}^2}}\)\(  = 10\sqrt 2 \,cm\);

- Thể tích  \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.10^2}.10 \)\(= \dfrac{1}{3} \cdot {10^3}\pi \left( {c{m^3}} \right).\)

+ Khi \(d = 10cm\) và \(h = 10cm\), ta có \(r = 5cm\);

- Đường sinh \(l = \sqrt {{h^2} + {r^2}}  = \sqrt {{{10}^2} + {5^2}}\)\(  = 5\sqrt 5 \,\left( {cm} \right)\);

- Thể tích \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}.\pi {.5^2}.10 \)\(= \dfrac{1}{3}250\pi \left( {c{m^3}} \right)\).

+ Khi \(h = 10cm\) và \(V = 1000\,c{m^3}\), ta có  \({r^2} = \dfrac{{3V}}{{\pi h}} = \dfrac{{3.1000}}{{\pi .10}} = \dfrac{{300}}{\pi }\)

\( \Rightarrow r = \sqrt {\dfrac{{300}}{{3,14}}}  = 9,77\left( {cm} \right),\)\(d = 2r = 19,54\left( {cm} \right).\)

- Đường sinh \(l = \sqrt {{h^2} + {r^2}}  = \sqrt {100 + \dfrac{{300}}{\pi }}\)\(  \approx 13,98cm\)

+ Khi \(r = 10cm\) và \(V = 1000\,c{m^3}\), ta có \(d = 2r = 20\left( {cm} \right);\)

- Chiều cao \(h = \dfrac{{3V}}{{\pi {r^2}}} = \dfrac{{3.1000}}{{\pi {{.10}^2}}} = 9,5\left( {cm} \right);\)

- Đường sinh \(l = \sqrt {\dfrac{{900}}{\pi } + 100}  \approx 19,66cm.\)

+ Khi \(d = 10cm\) và \(V = 1000c{m^3}\) ta có \(r = 5cm;\)

- Chiều cao  \(h = \dfrac{{3V}}{{\pi {r^2}}} = \dfrac{{3.1000}}{{\pi {{.5}^2}}} = \dfrac{{120}}{\pi }\left( {cm} \right);\)

 Đường sinh \(l = \sqrt {{r^2} + {h^2}}  = \sqrt {{5^2} + {{\left( {\dfrac{{120}}{\pi }} \right)}^2}}\)\(  \approx 38,5\left( {cm} \right).\)

Điền kết quả vào ô trống trong bảng trên.

Loigiaihay.com