Giải mục 2 trang 59, 60, 61, 62, 63 SGK Toán 12 tập 2 - Cùng khám pháCho hai đường thẳng d và d’ có các vectơ chỉ phương lần lượt là \(\overrightarrow a \) và \(\overrightarrow {a'} \), \({M_0} \in d\) như Hình 5.20. Quảng cáo
Lựa chọn câu để xem lời giải nhanh hơn
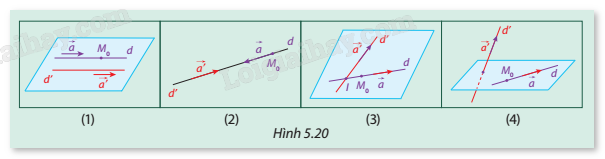
HĐ5 Trả lời câu hỏi Hoạt động 5 trang 59 SGK Toán 12 Cùng khám phá Cho hai đường thẳng d và d’ có các vectơ chỉ phương lần lượt là \(\overrightarrow a \) và \(\overrightarrow {a'} \), \({M_0} \in d\) như Hình 5.20.
Chọn các cụm từ thích hợp (song song, cắt nhau, chéo nhau, trùng nhau, cùng phương, không cùng phương, không có điểm chung, đúng một điểm chung, nhiều hơn một điểm chung cho các ô
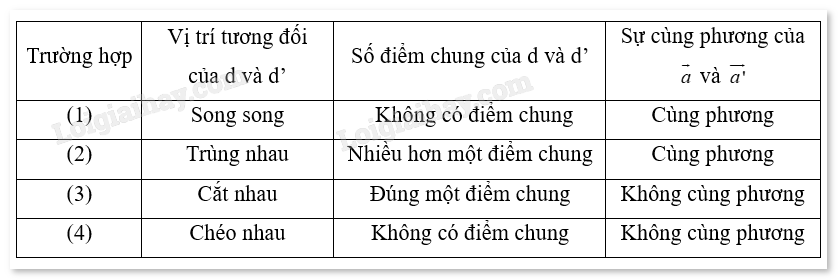
Phương pháp giải: - Song song: Hai đường thẳng song song nếu chúng cùng phương nhưng không cắt nhau. - Cắt nhau: Hai đường thẳng cắt nhau nếu chúng giao nhau tại một điểm và không cùng phương. - Chéo nhau: Hai đường thẳng chéo nhau nếu chúng không cùng nằm trên một mặt phẳng và không giao nhau. - Trùng nhau: Hai đường thẳng trùng nhau nếu chúng cùng phương và có vô số điểm chung. - Cùng phương: Hai đường thẳng cùng phương nếu vectơ chỉ phương của chúng cùng phương hoặc song song. Lời giải chi tiết:
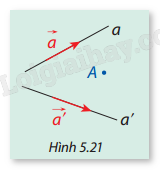
LT5 Trả lời câu hỏi Luyện tập 5 trang 62 SGK Toán 12 Cùng khám phá Trong không gian Oxyz, xét vị trí tương đối của các cặp đường thẳng sau: a) \(d:\left\{ {\begin{array}{*{20}{l}}{x = 3 - t}\\{y = 4 + t}\\{z = 5 - 2t}\end{array}} \right.\quad (t \in \mathbb{R})\) và \(d':\left\{ {\begin{array}{*{20}{l}}{x = 2 - 3t'}\\{y = 5 + 3t'}\\{z = 3 - 6t'}\end{array}} \right.\quad (t' \in \mathbb{R}){\rm{ }}\) b) \(d:\frac{{x - 1}}{1} = \frac{{y - 2}}{3} = \frac{{z - 3}}{{ - 1}}\) và \(d':\frac{{x - 2}}{{ - 2}} = \frac{{y + 2}}{1} = \frac{{z - 1}}{3}\) c) \(d:\left\{ {\begin{array}{*{20}{l}}{x = 1 + 2t}\\{y = 2 + t}\\{z = - 3 + 3t}\end{array}} \right.\quad (t \in \mathbb{R}){\rm{ }}\) và \(d':\frac{{x - 2}}{1} = \frac{{y + 3}}{2} = \frac{{z - 1}}{3}{\rm{ }}\) Phương pháp giải: - Hai đường thẳng song song: Nếu chúng có vectơ chỉ phương cùng phương và không có điểm chung. - Hai đường thẳng cắt nhau: Nếu chúng không cùng phương và có duy nhất một điểm chung. - Hai đường thẳng chéo nhau: Nếu chúng không nằm trong cùng một mặt phẳng và không có điểm chung. - Hai đường thẳng trùng nhau: Nếu chúng cùng phương và có vô số điểm chung. Lời giải chi tiết: a) - Vectơ chỉ phương của đường thẳng \(d\): \(\overrightarrow {{u_d}} = ( - 1;1; - 2)\) - Vectơ chỉ phương của đường thẳng\(d'\): \(\overrightarrow {{u_{d'}}} = ( - 3;3; - 6)\) Nhận thấy: \(\overrightarrow {{u_d}} = k\overrightarrow {{u_{d'}}} \) với \(k = \frac{1}{3}\) Vậy hai đường thẳng song song. b) - Vectơ chỉ phương của đường thẳng \(d\): \(\overrightarrow {{u_d}} = (1;3; - 1)\) - Vectơ chỉ phương của đường thẳng\(d'\): \(\overrightarrow {{u_{d'}}} = ( - 2;1;3)\) Nhận thấy không tồn tại giá trị k để \(\overrightarrow {{u_d}} = k\overrightarrow {{u_{d'}}} \) và \(\overrightarrow {{u_d}} .\overrightarrow {{u_{d'}}} = 1.( - 2) + 3.1 + ( - 1).3 = - 2 \ne 0\) nên hai đường thẳng không song song cũng không vuông góc. Để kiểm tra xem hai đường thẳng có cắt nhau không, ta giải hệ phương trình tham số từ hai đường thẳng. Phương trình tham số của \(d\): \(\frac{{x - 1}}{1} = \frac{{y - 2}}{3} = \frac{{z - 3}}{{ - 1}}\quad {\rm{hay}}\quad \left\{ {\begin{array}{*{20}{l}}{x = 1 + t}\\{y = 2 + 3t}\\{z = 3 - t}\end{array}} \right.\quad \quad t \in \mathbb{R}\) Phương trình tham số của \(d'\) \(\frac{{x - 2}}{{ - 2}} = \frac{{y + 2}}{1} = \frac{{z - 1}}{3}\quad {\rm{hay}}\quad \left\{ {\begin{array}{*{20}{l}}{x = 2 - 2t'}\\{y = - 2 + t'}\\{z = 1 + 3t'}\end{array}} \right.\quad \quad t' \in \mathbb{R}\) Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{1 + t = 2 - 2t'}\\{2 + 3t = - 2 + t'}\\{3 - t = 1 + 3t'}\end{array}} \right.\) Từ phương trình thứ nhất: \(t = 1 - 2t'\) Thay vào phương trình thứ hai: \(2 + 3(1 - 2t') = - 2 + t'\quad \Rightarrow \quad 5 - 6t' = - 2 + t'\quad \Rightarrow \quad 7 = 7t'\quad \Rightarrow \quad t' = 1\) Thay \(t' = 1\) vào \(t = 1 - 2t'\), ta có \(t = - 1\). Thay \(t = - 1\) và \(t' = 1\) vào phương trình thứ ba: \(3 - ( - 1) = 1 + 3(1)\quad \Rightarrow \quad 4 = 4\) Điều này đúng. Hai đường thẳng \(d\) và \(d'\) cắt nhau tại điểm \((x,y,z) = (0, - 1,4)\). c) - Vectơ chỉ phương của \(d\) là \(\overrightarrow {{u_d}} = (2,1,3)\). - Vectơ chỉ phương của \(d'\) là \(\overrightarrow {{u_{d'}}} = (1,2,3)\). \(\frac{2}{1} \ne \frac{1}{2} \ne \frac{3}{3}\) Do đó, \(d\) và \(d'\) không song song. Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{1 + 2t = 2 + t'}\\{2 + t = - 3 + 2t'}\\{ - 3 + 3t = 1 + 3t'}\end{array}} \right.\) Từ phương trình thứ nhất: \(t' = 2t - 1\). Thay vào phương trình thứ hai: \(t = \frac{7}{3}\), \(t' = \frac{{11}}{3}\). Thay vào phương trình thứ ba: Điều này sai Vậy hai đường thẳng \(d\) và \(d'\) chéo nhau. HĐ6 Trả lời câu hỏi Hoạt động 6 trang 62 SGK Toán 12 Cùng khám phá Trong không gian, cho hai đường thẳng a và a' lần lượt là giá của hai vectơ (khác \(\overrightarrow 0 \)) \(\vec a\) và \(\vec a'\) (Hình 5.21). Từ một điểm A bất kỳ, vẽ hai đường thẳng d và d' lần lượt song song với a và a'. a) Hỏi a và a' có phải lần lượt là vectơ chỉ phương của d và d' không? Vì sao? b) Nếu \(d \bot d'\), thì \(\vec a\) và \(\vec a'\) có vuông góc nhau không? Vì sao?
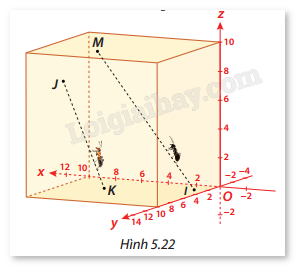
Phương pháp giải: Hai đường thẳng vuông góc nếu và chỉ nếu tích vô hướng của hai vectơ chỉ phương tương ứng bằng 0, nghĩa là: \(\vec a \cdot \vec a' = 0\) Lời giải chi tiết: a) Vectơ chỉ phương của d và d' là lần lượt \(\vec a\) và \(\vec a'\) vì các đường thẳng được kẻ song song với đường thẳng gốc a và a'. b) Nếu \(d \bot d'\), thì \(\vec a\) và \(\vec a'\) có vuông góc nhau. Điều này đúng vì tính vuông góc của hai đường thẳng tương ứng với tính vuông góc của hai vectơ chỉ phương, nghĩa là: \(\vec a \cdot \vec a' = 0\) LT6 Trả lời câu hỏi Luyện tập 6 trang 62 SGK Toán 12 Cùng khám phá Trong không gian Oxyz, tìm hai đường thẳng vuông góc nhau trong ba đường thẳng sau đây: \({d_1}:\frac{{x - 5}}{1} = \frac{{y + 3}}{2} = \frac{{z - 3}}{{ - 2}},\quad {d_2}:\frac{{x - 2}}{{ - 3}} = \frac{{y - 3}}{1} = \frac{{z - 1}}{6},\quad {d_3}:\left\{ {\begin{array}{*{20}{l}}{x = 1 - 2t}\\{y = 3}\\{z = 4 - t}\end{array}} \right.\) Phương pháp giải: - Tìm vectơ chỉ phương của các đường thẳng \({d_1},{d_2}\) và \({d_3}\). - Kiểm tra tích vô hướng giữa các cặp vectơ chỉ phương để tìm ra hai đường thẳng vuông góc. Lời giải chi tiết: - Đường thẳng \({d_1}\): vectơ chỉ phương \(\overrightarrow {{u_1}} = (1,2, - 2)\). - Đường thẳng \({d_2}\): vectơ chỉ phương \(\overrightarrow {{u_2}} = ( - 3,1,6)\). - Đường thẳng \({d_3}\): vectơ chỉ phương \(\overrightarrow {{u_3}} = ( - 2,0, - 1)\). - Tích vô hướng giữa \(\overrightarrow {{u_1}} = (1,2, - 2)\) và \(\overrightarrow {{u_2}} = ( - 3,1,6)\): \(\overrightarrow {{u_1}} \cdot \overrightarrow {{u_2}} = 1 \cdot ( - 3) + 2 \cdot 1 + ( - 2) \cdot 6 = - 3 + 2 - 12 = - 13\quad ({\rm{kh\^o ng vu\^o ng g\'o c}}).\) - Tích vô hướng giữa \(\overrightarrow {{u_1}} = (1,2, - 2)\) và \(\overrightarrow {{u_3}} = ( - 2,0, - 1)\): \(\overrightarrow {{u_1}} \cdot \overrightarrow {{u_3}} = 1 \cdot ( - 2) + 2 \cdot 0 + ( - 2) \cdot ( - 1) = - 2 + 0 + 2 = 0\quad ({\rm{vu\^o ng g\'o c}}).\) - Tích vô hướng giữa \(\overrightarrow {{u_2}} = ( - 3,1,6)\) và \(\overrightarrow {{u_3}} = ( - 2,0, - 1)\): \(\overrightarrow {{u_2}} \cdot \overrightarrow {{u_3}} = ( - 3) \cdot ( - 2) + 1 \cdot 0 + 6 \cdot ( - 1) = 6 + 0 - 6 = 0\quad ({\rm{vu\^o ng g\'o c}}).\) - Hai đường thẳng \({d_1}\) và \({d_3}\) vuông góc với nhau (do \(\overrightarrow {{u_1}} \cdot \overrightarrow {{u_3}} = 0\)). - Hai đường thẳng \({d_2}\) và \({d_3}\) cũng vuông góc với nhau (do \(\overrightarrow {{u_2}} \cdot \overrightarrow {{u_3}} = 0\)). VD2 Trả lời câu hỏi vận dụng 2 trang 63 SGK Toán 12 Cùng khám phá Trong không gian Oxyz cho trước (1 đơn vị = 1 cm), có một chú kiến vàng và một chú kiến đen bò trên hai sợi dây thẳng khác nhau. Giả sử tại thời điểm \(t\) (tính bằng phút), kiến vàng ở vị trí \((6 + t;8 - t;3 + t)\) trên đường thẳng \({d_1}\). Cùng thời điểm đó, kiến đen ở vị trí \((1 + t;2 + t;2t)\) trên đường thẳng \({d_2}\).
a) Chứng minh rằng hai chú kiến bò trên hai đường thẳng chéo nhau. b) Tính khoảng cách giữa hai chú kiến tại các thời điểm \(t = 0\) và \(t = 10\). c) Hỏi tại thời điểm nào thì khoảng cách giữa hai chú kiến là nhỏ nhất? Tính khoảng cách đó. Phương pháp giải: a) - Kiểm tra xem hai đường thẳng có song song không bằng cách so sánh vectơ chỉ phương. - Kiểm tra xem hai đường thẳng có cắt nhau không bằng cách giải hệ phương trình. b) Tại mỗi thời điểm t, tính tọa độ hai điểm trên hai đường thẳng tương ứng. Sử dụng công thức khoảng cách giữa hai điểm trong không gian 3 chiều: \(d = \sqrt {{{({x_2} - {x_1})}^2} + {{({y_2} - {y_1})}^2} + {{({z_2} - {z_1})}^2}} \) để tính khoảng cách giữa hai điểm tại các thời điểm yêu cầu. c) - Biểu diễn khoảng cách giữa hai điểm dưới dạng hàm theo t. - Sử dụng phương pháp tìm cực trị của hàm số (tính đạo hàm và giải phương trình đạo hàm bằng 0) để tìm giá trị t tại đó khoảng cách là nhỏ nhất. Lời giải chi tiết: a) - Vectơ chỉ phương của đường thẳng \({d_1}\) là: \(\overrightarrow {{u_1}} = (1, - 1,1)\). - Vectơ chỉ phương của đường thẳng \({d_2}\) là: \(\overrightarrow {{u_2}} = (1,1,2)\). Ta thấy hai vectơ chỉ phương \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không song song với nhau vì không có tỉ lệ giữa các tọa độ của hai vectơ. Vậy hai đường thẳng không song song. Để kiểm tra xem hai đường thẳng có cắt nhau không, ta viết phương trình vị trí của hai điểm trên đường thẳng: - Với \({d_1}\), điểm có tọa độ: \({M_1}(6 + t,8 - t,3 + t)\). - Với \({d_2}\), điểm có tọa độ: \({M_2}(1 + t,2 + t,2t)\). Giải hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{6 + t = 1 + t}\\{8 - t = 2 + t}\\{3 + t = 2t}\end{array}} \right.\) Hệ phương trình này không có nghiệm. Do đó, hai đường thẳng không cắt nhau nên hai đường thẳng chéo nhau. b) Tại \(t = 0\), tọa độ của hai chú kiến là: - Kiến vàng: \({M_1}(6,8,3)\). - Kiến đen: \({M_2}(1,2,0)\). Khoảng cách giữa hai chú kiến: \(d = \sqrt {{{(1 - 6)}^2} + {{(2 - 8)}^2} + {{(0 - 3)}^2}} = \sqrt {25 + 36 + 9} = \sqrt {70} \approx 8.37{\mkern 1mu} {\rm{cm}}.\) Tại \(t = 10\), tọa độ của hai chú kiến là: - Kiến vàng: \({M_1}(16, - 2,13)\). - Kiến đen: \({M_2}(11,12,20)\). Khoảng cách giữa hai chú kiến: \(d = \sqrt {{{(11 - 16)}^2} + {{(12 + 2)}^2} + {{(20 - 13)}^2}} = \sqrt {25 + 196 + 49} = \sqrt {270} \approx 16.43{\mkern 1mu} {\rm{cm}}.\) c) Khoảng cách giữa hai chú kiến là hàm số: \(d(t) = \sqrt {{{(1 + t - (6 + t))}^2} + {{(2 + t - (8 - t))}^2} + {{(2t - (3 + t))}^2}} .\) Rút gọn biểu thức: \(d(t) = \sqrt {{{( - 5)}^2} + {{( - 6 + 2t)}^2} + {{(t - 3)}^2}} = \sqrt {25 + {{( - 6 + 2t)}^2} + {{(t - 3)}^2}} .\) \(d(t) = \sqrt {25 + (4{t^2} - 24t + 36) + ({t^2} - 6t + 9)} = \sqrt {5{t^2} - 30t + 70} .\) Tìm giá trị nhỏ nhất của hàm số \(d(t)\) bằng cách tính đạo hàm: \(d'(t) = \frac{1}{{2\sqrt {5{t^2} - 30t + 70} }}(10t - 30) = 0.\) Giải phương trình: \(10t - 30 = 0\) cho \(t = 3\). Thay \(t = 3\) vào biểu thức khoảng cách: \(d(3) = \sqrt {5{{(3)}^2} - 30(3) + 70} = \sqrt {45 - 90 + 70} = \sqrt {25} = 5{\mkern 1mu} {\rm{cm}}.\) Vậy khoảng cách nhỏ nhất giữa hai chú kiến là 5 cm tại thời điểm \(t = 3\).
|




















Danh sách bình luận